
【题目】图1是一台实物投影仪,图2是它的示意图,折线![]() 表示固定支架,
表示固定支架,![]() 垂直水平桌面
垂直水平桌面![]() ,点
,点![]() 为旋转点,
为旋转点,![]() 可以旋转,当
可以旋转,当![]() 绕点
绕点![]() 逆时针旋转时,投影探头
逆时针旋转时,投影探头![]() 始终垂直于水平桌面
始终垂直于水平桌面![]() ,经测量:
,经测量:![]() ,
,![]() ,
,![]() ,
,![]() .(结果精确到
.(结果精确到![]() )
)
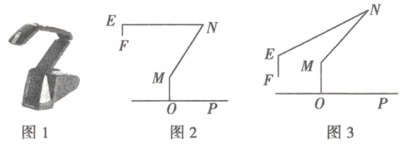
(1)如图2所示,![]() ,
,![]() .
.
①填空:![]() ;
;
②求投影探头的端点![]() 到桌面
到桌面![]() 的距离;
的距离;
(2)如图3所示,将(1)中的![]() 向下旋转,当投影探头的端点
向下旋转,当投影探头的端点![]() 到桌面
到桌面![]() 的距离为
的距离为![]() 时,求
时,求![]() 的大小.(参考数据
的大小.(参考数据![]() span>)
span>)
科目:初中数学 来源: 题型:
【题目】为了解九年级学生的体能状况,从我校九年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A,B,C,D四个等级,请根据两幅图中的信息回答下列问题:
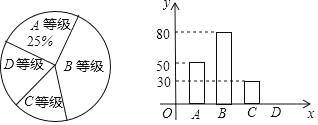
(1)求本次测试共调查了 名学生,补全条形统计图;
(2)B等级人数对应扇形统计图的圆心角的大小为 ;
(3)我校九年级共有2100名学生,请你估计九年级学生中体能测试结果为C等级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
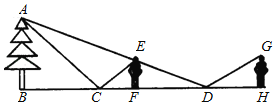
【题目】小明想用镜子测量一棵松树的高度,但因树旁有一条河,不能测量镜子与树之间的距离,于是他两次利用镜子,如图所示,第一次他把镜子放在C点,人在F点时正好在镜子中看到树尖A;第二次把镜子放在D点,人在G点正好看到树尖A.已知小明的眼睛距离地面1.70m,量得CD=12m,CF=1.8m,DH=3.8m.请你求出松树的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() ,若将
,若将![]() 先沿
先沿![]() 轴进行第一次对称变换,所得图形沿
轴进行第一次对称变换,所得图形沿![]() 轴进行第二次对称变换,轴对称变换的对称轴遵循
轴进行第二次对称变换,轴对称变换的对称轴遵循![]() 轴、
轴、![]() 轴、
轴、![]() 轴、
轴、![]() 轴…的规律进行,则经过第2018次变换后,
轴…的规律进行,则经过第2018次变换后,![]() 顶点
顶点![]() 坐标为()
坐标为()
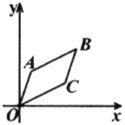
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列正多边形中,![]() 是中心,定义:
是中心,定义:![]() 为相应正多边形的基本三角形.如图1,
为相应正多边形的基本三角形.如图1,![]() 是正三角形
是正三角形![]() 的基本三角形;如图2,
的基本三角形;如图2,![]() 是正方形
是正方形![]() 的基本三角形;如图3,
的基本三角形;如图3,![]() 为正
为正![]() 边形
边形![]() …的基本三角形.将基本
…的基本三角形.将基本![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 角度得
角度得![]() .
.
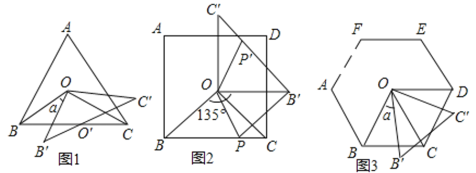
(1)若线段![]() 与线段
与线段![]() 相交点
相交点![]() ,则:
,则:
图1中![]() 的取值范围是________;
的取值范围是________;
图3中![]() 的取值范围是________;
的取值范围是________;
(2)在图1中,求证![]()
(3)在图2中,正方形边长为4,![]() ,边
,边![]() 上的一点
上的一点![]() 旋转后的对应点为
旋转后的对应点为![]() ,若
,若![]() 有最小值时,求出该最小值及此时
有最小值时,求出该最小值及此时![]() 的长度;
的长度;
(4)如图3,当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是反比例函数![]() 的图象,点
的图象,点![]() ,
,![]() 分别在图象的两支上,以
分别在图象的两支上,以![]() 为对角线作矩形
为对角线作矩形![]() 且
且![]() 轴.
轴.
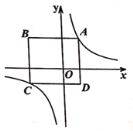
(1)当线段![]() 过原点时,分别写出
过原点时,分别写出![]() 与
与![]() ,
,![]() 与
与![]() 的一个等量关系式;
的一个等量关系式;
(2)当![]() 、
、![]() 两点在直线
两点在直线![]() 上时,求矩形
上时,求矩形![]() 的周长;
的周长;
(3)当![]() 时,探究
时,探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD中,AB∥CD,∠B=90°,AB=2CD.动点P从点A出发,在四边形ABCD的边上沿A→B→C的方向以1cm/s的速度匀速移动,到达点C时停止移动。已知△APD的面积S(cm 2)与点P运动的时间t(s)之间的函数图象如图②所示,根据题意解答下列问题
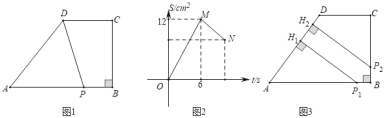
(1)在图①中,AB= cm, BC= cm.
(2)求图2中线段MN的函数关系式(并写出t的取值范围) .
(3)如图③,设动点P用了t1 (s)到达点P1处,用了t2 (s)到达点P2处,分别过P1、P2作AD的垂线,垂足为H1、H2.当P1H1= P2H2=4时,连P1P2,求△BP1P2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
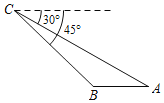
【题目】如图,已知点C处有一个高空探测气球,从点C处测得水平地面上A,B两点的俯角分别为30°和45°.若AB=2km,则A,C两点之间的距离为_____km.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com