
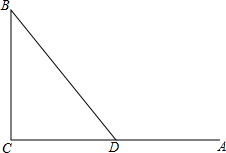
 如图,A、B、C三个地点(图中的线段均是道路),AC⊥BC,甲、乙两人同时从A地出发,已知甲的速度比乙的速度快$\frac{1}{4}$,如果经C地到达B地,且使乙比甲早到B地,这是一个不可能的情况,但在距A地200米的D处有一条路可直通B地(即图中BD).
如图,A、B、C三个地点(图中的线段均是道路),AC⊥BC,甲、乙两人同时从A地出发,已知甲的速度比乙的速度快$\frac{1}{4}$,如果经C地到达B地,且使乙比甲早到B地,这是一个不可能的情况,但在距A地200米的D处有一条路可直通B地(即图中BD).分析 (1)根据三角形两边之和大于第三边,让乙由A到D到B,而甲由A到D到C到B,则乙比甲可能早到B地;
(2)设乙的速度为x米/分,则甲的速度为$\frac{5}{4}$x米/分,根据乙比甲早到1分钟,列出方程,解方程即可.
解答 解:(1)根据三角形两边之和大于第三边,让乙由A到D到B,而甲由A到D到C到B,则乙比甲可能早到B地;
(2)在直角△BCD中,∵sin∠BDC=$\frac{BC}{BD}$=$\frac{4}{5}$,
∴可设BC=4k,则BD=5k,
由勾股定理得CD=3k,
∵AC=BC,
∴200+3k=4k,
∴k=200,
∴BD=5k=1000,BC+CD=7k=1400.
设乙的速度为x米/分,则甲的速度为$\frac{5}{4}$x米/分,根据题意得
$\frac{200+1400}{\frac{5}{4}x}$-$\frac{200+1000}{x}$=1,
解得:x=80.
经检验,x=80是原方程的解.
所以$\frac{5}{4}$x=100.
答:甲的速度为100米/分,乙的速度为80米/分.
点评 本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.也考查了解直角三角形的应用及三角形三边关系.


科目:初中数学 来源: 题型:解答题
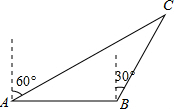 如图,海中有一灯塔C,它的周围11海里内有暗礁.一渔船以18海里/时的速度由西向东航行,在A点测得灯塔C位于北偏东60°的方向上,航行40分钟到达B点,此时测得灯塔C位于北偏东30°的方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
如图,海中有一灯塔C,它的周围11海里内有暗礁.一渔船以18海里/时的速度由西向东航行,在A点测得灯塔C位于北偏东60°的方向上,航行40分钟到达B点,此时测得灯塔C位于北偏东30°的方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com