
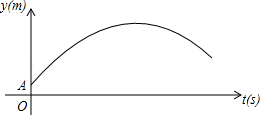
【题目】如图,某足球运动员站在点O处练习射门.将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,己知足球飞行0.8s时,离地面的高度为3.5m.
(1)a= ,c= ;
(2)当足球飞行的时间为多少时,足球离地面最高?最大高度是多少?
(3)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?
【答案】(1)![]() ,
,![]() ;(2)当足球飞行的时间
;(2)当足球飞行的时间![]() s时,足球离地面最高,最大高度是4.5m;(3)能.
s时,足球离地面最高,最大高度是4.5m;(3)能.
【解析】
(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),代入函数的表达式即可求出a,c的值;
(2)利用配方法即可求出足球飞行的时间以及足球离地面的最大高度;
(3)把x=28代入x=10t得t=2.8,把t=2.8代入解析式求出y的值和2.44m比较大小即可得到结论.
(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),
∴![]() ,
,
解得: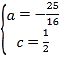 ,
,
∴抛物线的解析式为:y=﹣![]() t2+5t+
t2+5t+![]() ,
,
故答案为:﹣![]() ,
,![]() ;
;
(2)∵y=﹣![]() t2+5t+
t2+5t+![]() ,
,
∴y=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,y最大=4.5,
时,y最大=4.5,
∴当足球飞行的时间![]() s时,足球离地面最高,最大高度是4.5m;
s时,足球离地面最高,最大高度是4.5m;
(3)把x=28代入x=10t得t=2.8,
∴当t=2.8时,y=﹣![]() ×2.82+5×2.8+
×2.82+5×2.8+![]() =2.25<2.44,
=2.25<2.44,
∴他能将球直接射入球门.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点B,则k的值为( )
的图象经过点B,则k的值为( )
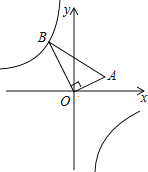
A.﹣2B.﹣4C.4D.﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线y1=-x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点
交于点A(1,m),这两条直线分别与x轴交于B,C两点
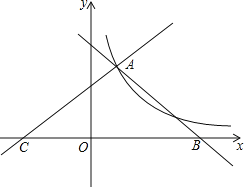
(1)求k的值;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP,且AP把△ABC的面积分成1:2两部分,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
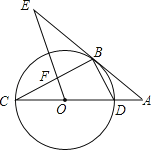
【题目】如图,CD是⊙O的直径,点B在⊙O上,连接BC、BD,直线AB与CD的延长线相交于点A,AB2=ADAC,OE∥BD交直线AB于点E,OE与BC相交于点F.
(1)求证:直线AE是⊙O的切线;
(2)若⊙O的半径为3,cosA=![]() ,求OF的长.
,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=(a2+1)x2+bx+c经过点A(﹣3,t)、B(4,t)两点,则不等式(a2+1)(x-2)2+bx<2b-c+t的解集是_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一放假期间,甲、乙、丙三位同学到某影城看电影,影城有A,B两部不同电影,甲、乙、丙3人分别从中任选一部观看,每部被选中的可能性相同.
(1)甲同学选择“A部电影”的概率为 ;
(2)用画树状图的方法求甲、乙、丙3人选择同一部电影的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形 ABCD 中,M,N,P,Q 分别为边 AB,BC,CD,DA 上的点(不与端点重合).对于任意矩形 ABCD,下面四个结论中:①存在无数个四边形 MNPQ 是平行四边形;②存在无数个四边形 MNPQ 是矩形;③存在无数个四边形 MNPQ 是菱形;④不存在四边形 MNPQ 是正方形.所有正确结论的序号是_________________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
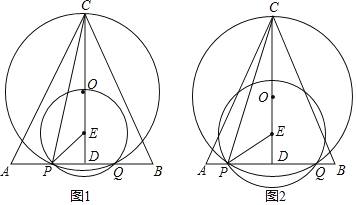
【题目】△ABC中,CA=CB,AB=![]() ,CD⊥AB于点D,CD=5,点O和点E在线段CD上,ED=1,点P在边AB上,以E为圆心,EP为半径的圆与AB边的另一个交点为点Q(点P在点Q的左侧),以O为圆心,OC为半径的圆O恰好经过P、Q两点,联结CP,设线段AP的长度为x.
,CD⊥AB于点D,CD=5,点O和点E在线段CD上,ED=1,点P在边AB上,以E为圆心,EP为半径的圆与AB边的另一个交点为点Q(点P在点Q的左侧),以O为圆心,OC为半径的圆O恰好经过P、Q两点,联结CP,设线段AP的长度为x.
(1)当圆E恰好经过点O时,求圆E的半径;
(2)联结CQ,设∠PCQ的正切值为y,求y与x的函数关系式及定义域;
(3)若∠PED=3∠PCE,求S△PCQ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径CD垂直弦AB于点E,且OE=DE.点P为![]() 上一点(点P不与点B,C重合),连结AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,
上一点(点P不与点B,C重合),连结AP,BP,CP,AC,BC.过点C作CF⊥BP于点F.给出下列结论:①△ABC是等边三角形;②在点P从B→C的运动过程中,![]() 的值始终等于
的值始终等于![]() .则下列说法正确的是( )
.则下列说法正确的是( )
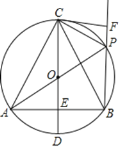
A.①,②都对B.①对,②错C.①错,②对D.①,②都错
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com