
 如图,在⊙O中,AB,CD为圆的两条弦,CD与OA,OB分别交于点E,F,且$\widehat{AC}=\widehat{BD}$,求证:OE=OF.
如图,在⊙O中,AB,CD为圆的两条弦,CD与OA,OB分别交于点E,F,且$\widehat{AC}=\widehat{BD}$,求证:OE=OF.  云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
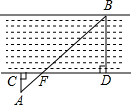 一条河的两岸有一段是互相平行的,为了测量河宽,王刚先站在河边观察对岸的一目标B,然后在岸边做一标记D,使BD垂直于河岸,再沿河岸走到点C,接着垂直河岸走到点A,使A,B和岸边的一点F在一条直线上.如果量得AC=5m,FD=20m,CF=4m,那么河宽BD有多少米?
一条河的两岸有一段是互相平行的,为了测量河宽,王刚先站在河边观察对岸的一目标B,然后在岸边做一标记D,使BD垂直于河岸,再沿河岸走到点C,接着垂直河岸走到点A,使A,B和岸边的一点F在一条直线上.如果量得AC=5m,FD=20m,CF=4m,那么河宽BD有多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
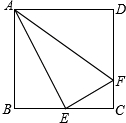 如图,正方形ABCD中,E是BC的中点,F是CD上的一点,EF⊥AE.
如图,正方形ABCD中,E是BC的中点,F是CD上的一点,EF⊥AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
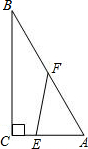 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E是直角边AC上动点(点E与A、C两点均不重合),点F是斜边AB上的动点(点F与A、B两点均不重合).设AE长为x.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E是直角边AC上动点(点E与A、C两点均不重合),点F是斜边AB上的动点(点F与A、B两点均不重合).设AE长为x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知正方形ABCD的边长为10,E(0,5),C(7,-5),一根细绳长155,从点E出发,顺时针绕在正方形上,将绳子的另一端到达的位置点F用坐标表示出来.
如图,已知正方形ABCD的边长为10,E(0,5),C(7,-5),一根细绳长155,从点E出发,顺时针绕在正方形上,将绳子的另一端到达的位置点F用坐标表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
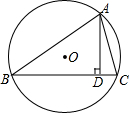 如图,O是△ABC的外心,AD是BC边上的高,R是△ABC外接圆的半径.问:
如图,O是△ABC的外心,AD是BC边上的高,R是△ABC外接圆的半径.问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com