
| A. | 1 | B. | $\frac{1}{2015}$ | C. | $\frac{2014}{2015}$ | D. | $\frac{2015}{2016}$ |
分析 首先求出抛物线与x轴两个交点坐标,然后由题意得到AnBn=$\frac{1}{n}$-$\frac{1}{n+1}$,进而求出A1B1+A2B2+…+A2015B2015的值.
解答 解:令y=x2-$\frac{2n+1}{n(n+1)}$x+$\frac{1}{n(n+1)}$=0,
即x2-$\frac{2n+1}{n(n+1)}$x+$\frac{1}{n(n+1)}$=0,
解得x=$\frac{1}{n}$或x=$\frac{1}{n+1}$,
故抛物线y=x2-$\frac{2n+1}{n(n+1)}$x+$\frac{1}{n(n+1)}$与x轴的交点为($\frac{1}{n}$,0),($\frac{1}{n+1}$,0),
由题意得AnBn=$\frac{1}{n}$-$\frac{1}{n+1}$,
则A1B1+A2B2+…+A2015B2015=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$=1-$\frac{1}{2016}$=$\frac{2015}{2016}$,
故选D.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是用n表示出抛物线与x轴的两个交点坐标,此题难度不大.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
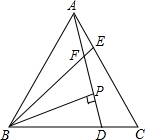 如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.
如图,已知△ABC为等边三角形,AE=CD,AD、BE相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
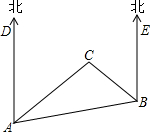 如图,是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西30°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?
如图,是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西30°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).
某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com