
【题目】如图1,在平面直角坐标系中,点A(﹣![]() ,0),B(
,0),B(![]() ,0),C(0,
,0),C(0,![]() ).D,E分别是线段AC和CB上的点,CD=CE.将△CDE绕点C逆时针旋转一个角度α.
).D,E分别是线段AC和CB上的点,CD=CE.将△CDE绕点C逆时针旋转一个角度α.
(1)若0°<α<90°,在旋转过程中当点A,D,E在同一直线上时,连接AD,BE,如图2.求证:AD=BE,且AD⊥BE
(2)若0°<α<360°,D,E恰好是线段AC和CB上的中点,在旋转过程中,当DE∥AC时,求α的值及点E的坐标.
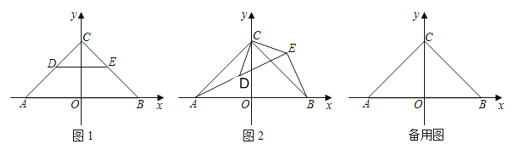
【答案】(1)证明见解析;(2)α=45°时,点E的坐标为(1,![]() );α=225°时,点E的坐标为(﹣1,
);α=225°时,点E的坐标为(﹣1,![]() )
)
【解析】
(1)证明△ACD≌△BCE,可得AD=BE,∠CAD=∠CBE,则结论得证;
(2)由勾股定理求出AC长,可求出CD 的长,如图1,当α=∠ACO=45°时,求出点E的坐标为(1,![]() ),如图2,当α=∠ACD=180°+∠ACO=225°时,求出点E的坐标为(﹣1,
),如图2,当α=∠ACD=180°+∠ACO=225°时,求出点E的坐标为(﹣1,![]() ).
).
(1)∵点A(﹣![]() ,0),B(
,0),B(![]() ,0),C(0,
,0),C(0,![]() ),
),
∴OC垂直平分AB,OA=OB=OC,
∴AC=BC,∠CAB=∠CBA=45°,∠ACB=90°,
根据旋转的性质得,∠ACD=∠BCE,
又∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE,
∴∠BAE+∠ABE=(∠CAB﹣∠CAD)+(∠ABC+∠CBE)=90°,
∴∠AEB=180°﹣(∠BAE+∠ABE)=90°,即AD⊥BE;
(2)由(1)知,∠ACB=90°,AC=BC,
在Rt△AOC中,AC=![]() =2,
=2,
∵D,E是线段AC和CB上的中点,
∴![]() =1,
=1,
如图1,当α=∠ACO=45°时,即∠ACO=∠CDE=45°,
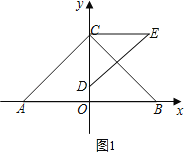
∴AC∥DE,
此时点E的坐标为(1,![]() ),
),
如图2,当α=∠ACD=180°+∠ACO=225°时,
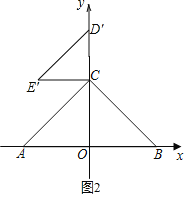
即∠ACO=∠CD′E′=45°,
∴AC∥D′E′,
此时点E的坐标为(﹣1,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如右图,正方形ABCD的边长为2,点E是BC边上一点,以AB为直径在正方形内作半圆
O,将△DCE沿DE翻折,点C刚好落在半圆O的点F处,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与直线
与直线![]() 交于A, B两点,其中点A在x轴上.
交于A, B两点,其中点A在x轴上.
(1)用含有b的代数式表示c;
(2)① 若点B在第一象限,且![]() ,求抛物线的解析式;
,求抛物线的解析式;
② 若![]() ,结合函数图象,直接写出b的取值范围.
,结合函数图象,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小芳家的落地窗(线段DE)与公路(直线PQ)互相平行,她每天做完作业后都会在点A处向窗外的公路望去.
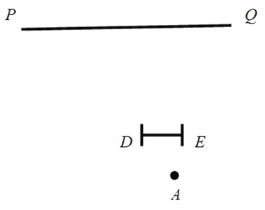
(1)请在图中画出小芳能看到的那段公路并记为BC.
(2)小芳很想知道点A与公路之间的距离,于是她想到了一个办法.她测出了邻家小彬在公路BC段上走过的时间为10秒,又测量了点A到窗的距离是4米,且窗DE的长为3米,若小彬步行的平均速度为1.2米/秒,请你帮助小芳计算出点A到公路的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2,我们来进行以下的探索:
)2,我们来进行以下的探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n都是正整数),则有a+b
)2(其中a,b,m,n都是正整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn,这样就得出了把类似a+b
,∴a=m2+2n2,b=2mn,这样就得出了把类似a+b![]() 的式子化为平方式的方法,请仿照上述方法探索并解决下列问题:
的式子化为平方式的方法,请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m,n的式子分别表示a,b,得a= ,b= .
)2,用含m,n的式子分别表示a,b,得a= ,b= .
(2)若a﹣4![]() =(m﹣n
=(m﹣n![]() )2且a,m,n都为正整数,求a的值.
)2且a,m,n都为正整数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
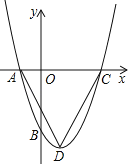
【题目】如图,抛物线y=x2+bx+c与x轴交于A,C两点,与y轴交于B点,抛物线的顶点为点D,已知点A的坐标为(﹣1,0),点B的坐标为(0,﹣3).
(1)求抛物线的解析式及顶点D的坐标.
(2)求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() 是整数).
是整数).
(1)求证:方程有两个不相等的实数根;
(2)若方程的两个实数根分别为![]() ,
,![]() (其中
(其中![]() ),设
),设![]() ,则
,则![]() 是否为变量
是否为变量![]() 的函数?如果是,求出函数的解析式;如果不是,请说明理由.
的函数?如果是,求出函数的解析式;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年北疆承办了世界园艺博览会,某商店为了抓住博览会的商机,决定购买A.B两种世园会纪念品,若购进A中纪念品20件,B种纪念品10件,需要2000元;若购进A中纪念品8件,B种纪念品6件,需要1100元.
(1)求购进A.B两种纪念品每件各需要多少元?
(2)若该商店决定拿出10000元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量不少于B种的6倍,且少于B种纪念品数量的8倍,设购进B种纪念品a件,则该商店共有几种进货方案?
(3)在第(2)问的条件下,若销售每件A种纪念品可获利润30元,每件B种纪念品可获利润40元,设总利润为y元,请写出总利润y(元)与a(个)的函数关系式,并根据函数关系式说明总利润最高时的进货方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com