
 .设四边形ABPQ关于直线x=t的对称的图形与△QPC重叠
.设四边形ABPQ关于直线x=t的对称的图形与△QPC重叠
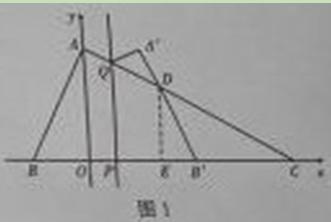

 由对称性可知,∠ABO=∠DB’E,又∵∠AOB=∠DEB’
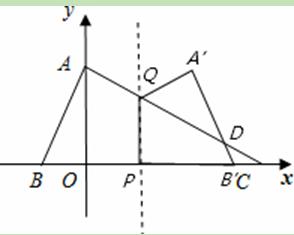
由对称性可知,∠ABO=∠DB’E,又∵∠AOB=∠DEB’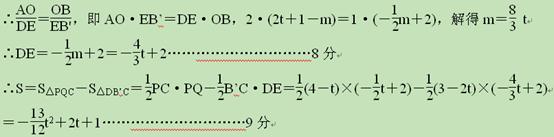 ②当1.5≤t<4时,点B’在点C的右侧或与点C重合(如图2)
②当1.5≤t<4时,点B’在点C的右侧或与点C重合(如图2)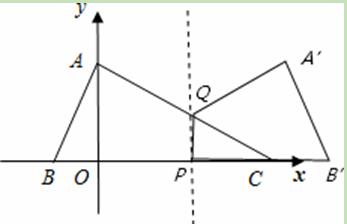
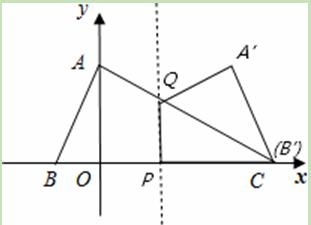
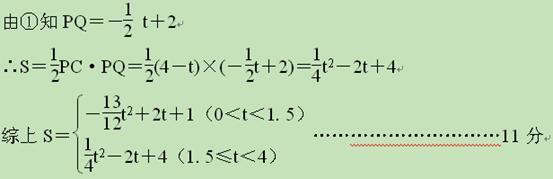 另外的解法:如图,当1.5≤t<4时,重合部分为三角形△CPQ,如图2
另外的解法:如图,当1.5≤t<4时,重合部分为三角形△CPQ,如图2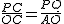 ,
,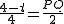 ,
,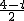 .
.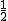 (4-t)
(4-t)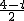 =
=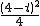 (1.5<t≤4),
(1.5<t≤4),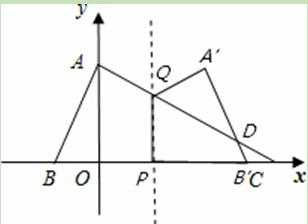
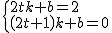 ,
,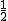 x+2和y=-x+(2+4t)组成方程组得
x+2和y=-x+(2+4t)组成方程组得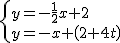 ,
, ,
, 2t+1,0),C点坐标为(4,0),
2t+1,0),C点坐标为(4,0),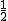 (4-t)
(4-t)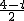 =
=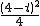 ,
,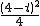 -
-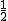 (3-2t)(-4t+2)=-
(3-2t)(-4t+2)=-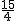 t2+6t+1(0<t≤1.5).
t2+6t+1(0<t≤1.5).

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源:不详 题型:单选题
 ,
,  ,
,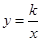 (x>0),当扫描线遇到黑色区域时,区
(x>0),当扫描线遇到黑色区域时,区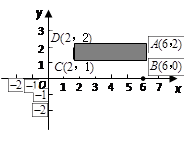
| A.4≤k≤6 | B.2≤k≤12 |
| C.6<k<12 | D.2<k<12 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com