
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx﹣3与直线y=x+3交于点A(m,0)和点B(2,n),与y轴交于点C.
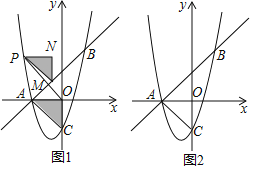
(1)求m,n的值及抛物线的解析式;
(2)在图1中,把△AOC平移,始终保持点A的对应点P在抛物线上,点C,O的对应点分别为M,N,连接OP,若点M恰好在直线y=x+3上,求线段OP的长度;
(3)如图2,在抛物线上是否存在点Q(不与点C重合),使△QAB和△ABC的面积相等?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=x2+2x﹣3,m=﹣3,n=5;(2)3![]() 或
或![]() ;(3)存在;Q点坐标为(﹣1,﹣4)或(3,12)或(﹣4,5),理由见解析
;(3)存在;Q点坐标为(﹣1,﹣4)或(3,12)或(﹣4,5),理由见解析
【解析】
(1)把点A(m,0)和点B(2,n)代入直线y=x+3,解得:m=﹣3,n=5,A(﹣3,0)、B(2,5),把A、B坐标代入抛物线解析式即可求解;
(2)由平移得:PN=OA=3,NM=OC=3,设:平移后点P(t,t2+2t﹣3),则N(t+3,t2+2t﹣3),M(t+3,t2+2t﹣6),根据点M在直线y=x+3上,即可求解;
(3)存在.设:直线AB交y轴于D(0,3),点C关于点D的对称点为C′(0,9)按照△QAB和△Q′AB和△ABC的面积相同即可求解.
解:(1)把点A(m,0)和点B(2,n)代入直线y=x+3,解得:m=﹣3,n=5,
∴A(﹣3,0)、B(2,5),把A、B坐标代入抛物线解析式,解得:a=1,b=2,
∴抛物线解析式为:y=x2+2x﹣3…①,
则C(0,﹣3);
(2)由平移得:PN=OA=3,NM=OC=3,
设:平移后点P(t,t2+2t﹣3),则N(t+3,t2+2t﹣3),
∴M(t+3,t2+2t﹣6),∵点M在直线y=x+3上,
∴t2+2t﹣6=t+3+3,解得:t=3或﹣4,
∴P点坐标为(3,12)或(﹣4,5),
则线段OP的长度为:3![]() 或
或![]() ;
;
(3)存在.
设:直线AB交y轴于D(0,3),点C关于点D的对称点为C′(0,9)
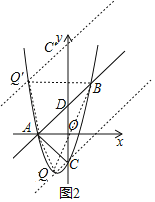
过点C和C′分别做AB的平行线,交抛物线于点Q、Q′,
则:△QAB和△Q′AB和△ABC的面积相同,
直线QC和Q′C的方程分别为:y=x﹣3和y=x+9…②,
将①、②联立,解得:x=﹣1或x=3或x=﹣4,
∴Q点坐标为(﹣1,﹣4)或(3,12)或(﹣4,5).


科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
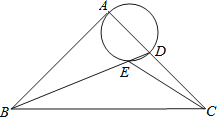
【题目】如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=4![]() ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为___.
,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
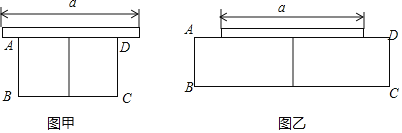
【题目】某植物园有一块足够大的空地,其中有一堵长为a米的墙,现准备用20米的篱笆围两间矩形花圃,中间用篱笆隔开.小俊设计了如图甲和乙的两种方案:
方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长.
(1)若a=6.
①按图甲的方案,要围成面积为25平方米的花圃,则AD的长是多少米?
②按图乙的方案,能围成的矩形花圃的最大面积是多少?
(2)若0<a<6.5,哪种方案能围成面积最大的矩形花圃?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西昌市数科科如局从2013年起每年对全市所有中学生进行“我最喜欢的阳光大课间活动”抽样调查(被调查学生每人只能选一项),并将抽样调查的数据绘制成图1、图2两幅统计图,根据统计图提供的信息解答下列问题:
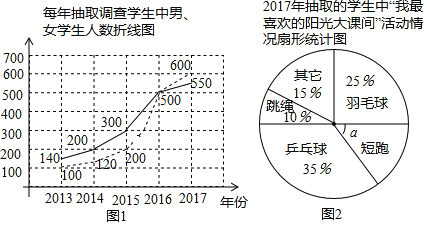
(1) 年抽取的调查人数最少; 年抽取的调查人数中男生、女生人数相等;
(2)求图2中“短跑”在扇形图中所占的圆心角α的度数;
(3)2017年抽取的学生中,喜欢羽毛球和短跑的学生共有多少人?
(4)如果2017年全市共有3.4万名中学生,请你估计我市2017年喜欢乒乓球和羽毛球两项运动的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A,B两地相向匀速行驶,甲车先出发两小时,甲车到达B地后立即调头,并保持原速度与乙车同向行驶,乙车到达A地后,继续保持原速向远离B的方向行驶,经过一段时间后两车同时到达C地,设两车之间的距离为y(干米),甲车行驶的时间为x小时,y与x之间的函数图象如图所示,则当甲车重返A地时,乙车距离C地________千米.
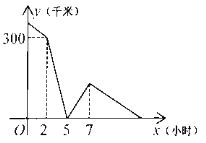
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xoy中,二次函数![]() 的图象与x轴的交点为A,B,顶点为C,点D为点C关于x轴的对称点,过点A作直线l:
的图象与x轴的交点为A,B,顶点为C,点D为点C关于x轴的对称点,过点A作直线l:![]() 交BD于点E,连接BC的直线交直线l于K点.
交BD于点E,连接BC的直线交直线l于K点.
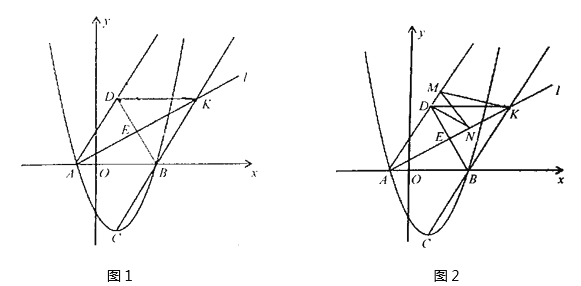
(1)问:在四边形ABKD内部是否存在点P,使它到四边形ABKD四边的距离都相等?
若存在,请求出点P的坐标;若不存在,请说明理由;
(2)若M,N分别为直线AD和直线l上的两个动点,连结DN,NM,MK,如图2,求DN+NM+MK和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD:OD=2:1,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.
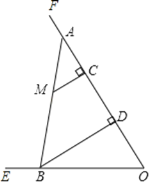
(1)当AC的长度为多少时,△AMC和△BOD相似;
(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;
(3)连结BC.当S△AMC=S△BOC时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
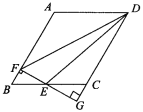
【题目】已知:如图,□ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B点重合),作EF⊥AB于F,FE,DC的延长线交于点G,设BE=x,△DEF的面积为S.
(1)求证:△BEF∽△CEG;
(2)求用x表示S的函数表达式,并写出x的取值范围;
(3)当E点运动到何处时,S有最大值,最大值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com