
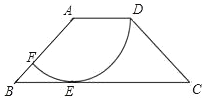
 如图,在四边形ABCD中,AD∥BC,AD=2,AB=2$\sqrt{2}$,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
如图,在四边形ABCD中,AD∥BC,AD=2,AB=2$\sqrt{2}$,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.分析 (1)连接AE,利用勾股定理得AE=BE,由此即可求出∠ABE的度数;
(2)首先求出扇形的圆心角∠DAB的度数,再由弧长公式:弧长=$\frac{nπR}{180}$求出弧长,此弧长就是所得圆锥的底面圆的周长,由圆的周长公式即可求得所得圆锥的底面半径.
解答 解:(1)连接AE,如图1,∵AD为半径的圆与BC相切于点E,
∴AE⊥BC,AE=AD=2.在Rt△AEB中,∵AB=2$\sqrt{2}$,AE=2,由勾股定理得AE=BE,
∴∠ABE=45°.
图1
(2)∵AD∥BC,∴∠DAB+∠ABE=180°,∴∠DAB=135°,
∴扇形A-BEF的弧长=$\frac{nπR}{180}$=$\frac{3π}{2}$.
设所得圆锥的底面半径是r,
则:2πr=$\frac{3π}{2}$,
∴r=0.75.
即:所得圆锥的底面半径是0.75
点评 本题考查了切线的性质、平行线的性质、圆锥的计算,解题的关键是掌握所涉及的知识要点,并能够灵活运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
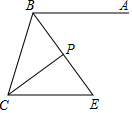 已知:如图AB∥CE,BE平分∠ABC,CP平分∠BCE交BE于点P.
已知:如图AB∥CE,BE平分∠ABC,CP平分∠BCE交BE于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
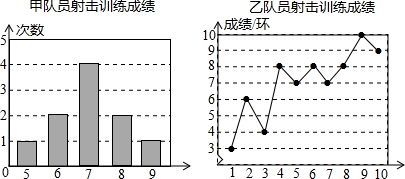
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | a | 7 | 7 | c |
| 乙 | 7 | b | 8 | 4.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
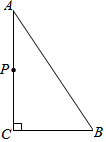 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在边长为8的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
已知:如图,在边长为8的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com