
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O,点O关于直线CD的对称点为E,连接DE,CE.

(1)求证:四边形ODEC为菱形;
(2)连接OE,若BC=2![]() ,求OE的长.
,求OE的长.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】六张形状大小完全相同的小长方形卡片,分两种不同形式不重叠的放在一个底面长为m,宽为n的长方形盒子底部(如图①、图②),盒子底面未被卡片覆盖的部分用阴影表示,设图①中阴影图形的周长为![]() ,图②中两个阴影部分图形的周长和为
,图②中两个阴影部分图形的周长和为![]() 则用含m、n的代数式
则用含m、n的代数式![]() =_______,
=_______,![]() =_______,若
=_______,若![]() ,则m=_____(用含n的代数式表示)
,则m=_____(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() x+2与x轴交于点A,与y轴交于点C,抛物线y=
x+2与x轴交于点A,与y轴交于点C,抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.

(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点;
①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1, △BCE的面积为S2, 求![]() 的最大值;
的最大值;
②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
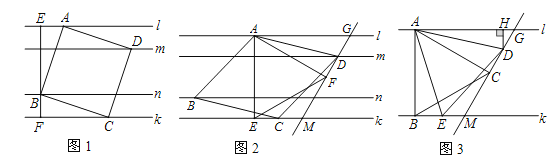
【题目】【背景】已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1,d2,d3,且d1=d3=1,d2=2.我们把四个顶点分别在l,m,n,k这四条平行线上的四边形称为“格线四边形” .
【探究1】(1)如图1,正方形ABCD为“格线四边形”,BE⊥l于点E,BE的反向延长线交直线k于点F.求正方形ABCD的边长.
【探究2】(2)如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E,∠AFD=90°,直线DF分别交直线l,k于点G、点M.求证:EC=DF.
【拓展】(3)如图3,l∥k,等边△ABC的顶点A,B分别落在直线l,k上,AB⊥k于点B,且∠ACD=90°,直线CD分别交直线l、k于点G、点M,点D、点E分别是线段GM、BM上的动点,且始终保持AD=AE,DH⊥l于点H.猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙两个空调安装队分别为A、B两个公司安装空调,甲安装队为A公司安装66台空调,乙安装队为B公司安装60台空调,甲、乙两队安装空调所用的总时间相同.已知甲队比乙队平均每天多安装2台空调,求甲、乙两个安装队平均每天各安装空调的台数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅开车到某地送货,汽车出发前油箱中有油50升,行驶一段时间,张师傅在加油站加油,然后继续向目的地行驶.已知加油前、后汽车都匀速行驶,汽车行驶时每小时的耗油量一定.油箱中剩余油量Q(升)与汽车行驶时间t(时)之间的函数图象如图所示.

(1)张师傅开车行驶________小时后开始加油,本次加油________升.
(2)求加油前Q与t之间的函数关系式.
(3)如果加油站距目的地210千米,汽车行驶速度为70千米/时,张师傅要想到达目的地,油箱中的油是否够用?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”n的各个数位上的数字之和记为F(n).例如n=135时,F(135)=1+3+5=9.
(1)对于“相异数”n,若F(n)=6,请你写出一个n的值;
(2)若a,b都是“相异数”,其中a=100x+12,b=350+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=![]() ,当F(a)+F(b)=18时,求k的最小值.
,当F(a)+F(b)=18时,求k的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
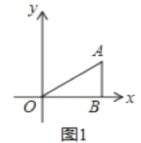
【题目】如图1,在平面直角坐标系中,点O为坐标原点,点A(3a,2a)在第一象限,过点A向x轴作垂线,垂足为点B,连接OA,S△AOB=12,点M从O出发,沿y轴的正半轴以每秒2个单位长度的速度运动,点N从点B出发以每秒3个单位长度的速度向x轴负方向运动,点M与点N同时出发,设点M的运动时间为t秒,连接AM,AN,MN.
(1)求a的值;
(2)当0<t<2时,
①请探究∠ANM,∠OMN,∠BAN之间的数量关系,并说明理由;
②试判断四边形AMON的面积是否变化?若不变化,请求出其值;若变化,请说明理由。
(3)当OM=ON时,请求出t的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com