在数学活动课上，王老师发给每位同学一张半径为6个单位长度的圆形纸板，要求同学们：（1）从带刻度的三角板、量角器和圆规三种作图工具中任意选取作图工具，把圆形纸板分成面积相等的四部分；（2）设计的整个图案是某种对称图形.王老师给出了方案一，请你用所学的知识再设计两种方案，并完成下面的设计报告.
| 名 称 | 四等分圆的面积 | ||
| 方 案 | 方案一 | 方案二 | 方案三 |
| 选用的工具 | 带刻度的三角板 | ||
|
|
|
|
|
| 简述设计方案 | 作⊙O两条互相垂直的直径AB、CD，将⊙O的面积分成相等的四份. | ||
| 指出对称性 | 既是轴对称图形又是中心对称图形 |
| 四等分圆的面积 | |||
| 方案 | 方案一 | 方案二 | 方案三 |
| 选用的工具 | 带刻度的三角板 | 带刻度三角板、量角器、圆规. | 带刻度三角板、圆规. |
|
|
|
|
|
| 简述设计方案 | 作⊙O两条互相垂直的直径AB、CD，将⊙O的面积分成相等的四份. | ⑴以点O为圆心，以3个单位长度为半径作圆； ⑵在大⊙O上依次取三等分点A、B、C； （3）连接OA、OB、OC. 则小圆O与三等份圆环把⊙O的面积四等分. | （4）作⊙O的一条直径AB; （5）分别以OA、OB的中点为圆心，以3个单位长度为半径作⊙O1、⊙O2； 则⊙O1、⊙O2和⊙O中剩余的两部分把⊙O的面积四等分。 |
| 指出对称性 | 既是轴对称图形又是中心对称图形. | 轴对称图形 | 既是轴对称图形又是中心对称图形. |
科目：初中数学 来源： 题型：
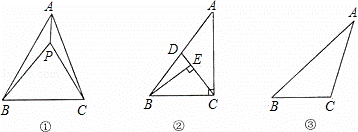
如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．
（1）如图②，已知Rt△ABC中，∠ACB=90°，∠ABC＞∠A，CD是AB上的中线，过点B作BE丄CD，垂足为E．试说明E是△ABC的自相似点；（4分）
（2）在△ABC中，∠A＜∠B＜∠C．
①如图③，利用尺规作出△ABC的自相似点P（不写出作法，留作图痕迹）；（3分）
②若△ABC的内心P是该三角形的自相似点，求该三角形三个内角的度数．（3分）
查看答案和解析>>
科目：初中数学 来源： 题型：
“如果二次函数y＝ax2＋bx＋c的图象与x轴有两个公共点，那么一元二次方程ax2＋bx＋c=0有两个不相等的实数根.”请根据你对这句话的理解，解决下面问题：
若m、n（m<n）是关于x的方程
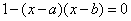的两根，且a < b， 则a、b、m、n 的大小关系是
A. m < a < b< n B. a < m < n < b C. a < m < b< n D. m < a < n < b
查看答案和解析>>
科目：初中数学 来源： 题型：
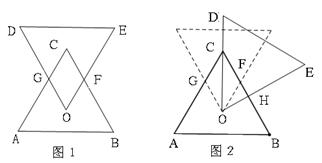
如图（1），有两个全等的正三角形ABC和ODE，点O、C分别为△ABC、△DEO的重心；固定点O，将△ODE顺时针旋转，使得OD 经过点C，如图（2）所示，则图（2）中四边形OGCF与△OCH面积的比为 .
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，⊙
，⊙
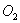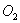的圆心，都在直线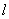
上，且半径分别为2cm，3cm，
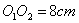.若⊙以1cm/s的速度沿直线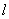向右匀速运动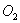（⊙保持静止），则在7s时刻⊙与⊙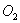的位置关系是
A．外切 B．相交 C．内含 D．内切
查看答案和解析>>
科目：初中数学 来源： 题型：
把一条12个单位长度的线段分成三条线段，其中一条线段长为4个单位长度，另两条线段长都是单位长度的整数倍。
（1）不同分法得到的三条线段能组成多少个不全等的三角形？用尺规作出这些三角形（用给定的单位长度，不写作法，保留作图痕迹
）；
（2）求出（1）中所作三角形外接圆的周长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
画出示意图
单位：cm）则该几何体的侧面积等于（ ）
B. 
C. 
D. 
