
【题目】已知方程x+![]() (c是常数,c≠0)的解是c或
(c是常数,c≠0)的解是c或![]() ,那么方程x+
,那么方程x+![]() (a是常数,且a≠0)的解是_____或_____.
(a是常数,且a≠0)的解是_____或_____.
科目:初中数学 来源: 题型:
【题目】瑞士著名数学家欧拉发现:简单多面体的顶点数V、面数F及棱数E之间满足一种有趣的关系:V+F﹣E=2,这个关系式被称为欧拉公式.比如:正二十面体(如右图),是由20个等边三角形所组成的正多面体,已知每个顶点处有5条棱,则可以通过欧拉公式算出正二十面体的顶点为_____个.那么一个多面体的每个面都是五边形,每个顶点引出的棱都有3条,它是一个_____面体.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的个数是( )
①若三条线段的比为1:1:![]() ,则它们组成一个等腰直角三角形
,则它们组成一个等腰直角三角形
②当四边形对角线垂直时连四边形各边中点得到一个矩形
③对角线互相垂直的四边形是菱形;
④一条对角线平分一组对角线的平行四边形为菱形;
⑤过矩形对角线交点的一条直线与矩形的一组对边相交,必分矩形为面积相等的两部分.
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是( )
①甲骑车速度为30km/小时,乙的速度为20km/小时;
②l1的函数表达式为y=80﹣30x;
③l2的函数表达式为y=20x;
④![]() 小时后两人相遇.
小时后两人相遇.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】典典同学学完统计知识后,随机调查了她家所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:
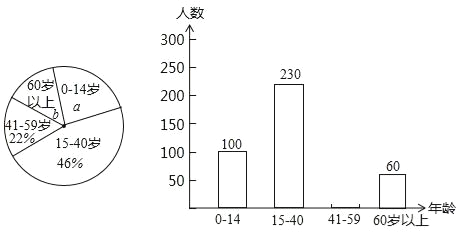
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3)一天,典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分不低于乙组得分的1.5倍,甲组得分最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线.
(2)若∠B=30°,AB=8,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.

(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com