
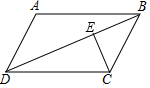
 如图,在平行四边形ABCD中,对角线BD=14cm,CE⊥BD,垂足为点E,且CE=5cm,AD=7cm,则AD与BC之间的距离为10cm.
如图,在平行四边形ABCD中,对角线BD=14cm,CE⊥BD,垂足为点E,且CE=5cm,AD=7cm,则AD与BC之间的距离为10cm. 分析 利用等积法,设AD与BC之间的距离为h,由条件可知?ABCD的面积是△BCD的面积的2倍,可求得?ABCD的面积,再由S四边形ABCD=AD•h,可求得h.
解答 解:∵四边形ABCD为平行四边形,
∴AB=CD,AD=BC,
在△BCD和△DAB中,
$\left\{\begin{array}{l}{BC=DA}\\{DC=BA}\\{BD=DB}\end{array}\right.$,
∴△BCD≌△DAB(SSS),
∵CE⊥BD,BD=14cm,CE=5cm,
∴S△BCD=$\frac{1}{2}$BD•CE=$\frac{1}{2}$×14×5=35(cm2),
∴S四边形ABCD=2S△BCD=70cm2,
设AD与BC之间的距离为hcm,
则S四边形ABCD=AD•h=7h,
∴7h=70,
解得h=10.
故答案为:10.
点评 本题主要考查平行四边形的性质,由条件得到四边形ABCD的面积是△BCD的面积的2倍是解题的关键,再借助等积法求解使解题事半功倍.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:选择题
| A. | m=-4 | B. | m=4 | C. | m≥4 | D. | m≤-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
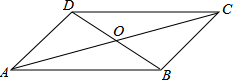 如图,在四边形ABCD中,对角线AC与BD交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )
如图,在四边形ABCD中,对角线AC与BD交于点O,下列条件中不一定能判定这个四边形是平行四边形的是( )| A. | AB∥DC,AD=BC | B. | AD∥BC,AB∥DC | C. | AB=DC,AD=BC | D. | OA=OC,OB=OD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$ | B. | $\frac{6}{11}$ | C. | $\frac{5}{11}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
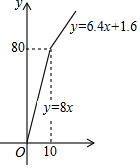 某书定价8元,如果一次购买10本以上,超过10本部分打八折,那么付款金额y与购书数量x之间的函数关系如何,同学们对此展开了讨论:
某书定价8元,如果一次购买10本以上,超过10本部分打八折,那么付款金额y与购书数量x之间的函数关系如何,同学们对此展开了讨论:| 购买量/本 | 1 | 2 | 3 | 4 | … | 9 | 10 | 11 | 12 | … |
| 付款金额/元 | 8 | 16 | 24 | 32 | … | 72 | 80 | 86.4 | 92.8 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com