
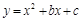 与x轴交于A、B两点(点A在点B的左侧),点B的坐标为
与x轴交于A、B两点(点A在点B的左侧),点B的坐标为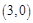 ,与y轴交于点
,与y轴交于点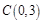 ,顶点为D。
,顶点为D。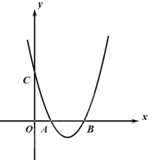
 .
. ,再过点A作AH⊥BC,垂足为H,利用tAn∠ACB=
,再过点A作AH⊥BC,垂足为H,利用tAn∠ACB= 求出即可.
求出即可. ,解得
,解得 ,
, ,
, ,
, ,
, .
.

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
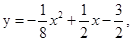 为什那么铅球运动过程中最高点离地面的距离____米。
为什那么铅球运动过程中最高点离地面的距离____米。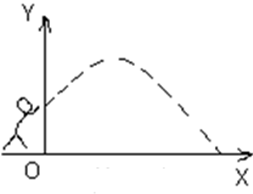
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).
),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
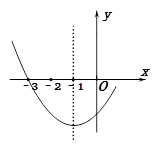
| A.①② | B.②③ | C.①②④ | D.②③④ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.ac<0 | B.2a+b=0 |
| C.4a+2b+c>0 | D.对于任意x均有ax2+bx≥a+b |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com