Question

如图1，Rt△ABC中AB=AC，点D、E是线段AC上两动点，且AD=EC，AM垂直BD，垂足为M，AM的延长线交BC于点N，直线BD与直线NE相交于点F．试判断△DEF的形状，并加以证明．
说明：（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；（2）在你经历说明（1）的过程之后，可以从下列①、②中选取一个补充或者更换已知条件，完成你的证明．
1、画出将△BAD沿BA方向平移BA长，然后顺时针旋转90°后图形；
2、点K在线段BD上，且四边形AKNC为等腰梯形（AC∥KN，如图2）．
附加题：如图3，若点D、E是直线AC上两动点，其他条件不变，试判断△DEF的形状，并说明理由．

Answer 1

解：△DEF是等腰三角形
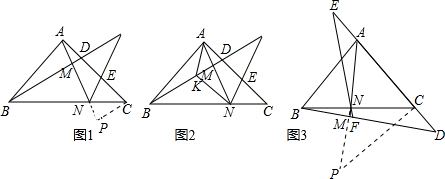
证明：如图，过点C作CP⊥AC，交AN延长线于点P
∵Rt△ABC中AB=AC
∴∠BAC=90°，∠ACB=45°
∴∠PCN=∠ACB，∠BAD=∠ACP
∵AM⊥BD
∴∠ABD+∠BAM=∠BAM+∠CAP=90°
∴∠ABD=∠CAP
∴△BAD≌△ACP
∴AD=CP，∠ADB=∠P
∵AD=CE
∴CE=CP
∵CN=CN
∴△CPN≌△CEN
∴∠P=∠CEN
∴∠CEN=∠ADB
∴∠FDE=∠FED
∴△DEF是等腰三角形．

附加题：△DEF为等腰三角形
证明：过点C作CP⊥AC，交AM的延长线于点P
∵Rt△ABC中AB=AC
∴∠BAC=90°，∠ACB=45°
∴∠PCN=∠ACB=∠ECN
∵AM⊥BD
∴∠ABD+∠BAM=∠BAM+∠CAP=90°
∴∠ABD=∠CAP
∴△BAD≌△ACP
∴AD=CP，∠D=∠P
∵AD=EC，CE=CP
又∵CN=CN
∴△CPN≌△CEN
∴∠P=∠E
∴∠D=∠E
∴△DEF为等腰三角形．
分析：（1）要证DF=EF，就要证出∠FDE=∠FED，也就是∠BDA=∠NEC，观察这两个角，不能直接用角的大小关系或全等来得出相等，那么可通过构建全等三角形来得出一个和两个分别相等的中间值，以此来证出两角相等，那么可过C作CP⊥AC，那么我们可通过证三角形ABD和APC全等来得出∠ADB=∠ACP，通过证三角形CPN和CEN全等来得出∠MEC=∠NPC．先看第一对三角形，已知的条件有AB=AD，一组直角，而∠ABD和∠PAC都是∠ADB的余角，因此∠ABD=∠PAD，那么两三角形就全等，可得出AC=PC=CE，∠ADB=∠NPC，又知道了∠NCE=∠PCN=45°，一条公共边CN，那么后面的一对三角形也全等，就能得出∠ADB=∠MEC=∠NPC，也就能得出∠FDE=∠FED了由此可得证．
（2）解题思路和（1）一样，也是先证三角形ABD和APC全等，后证三角形CPN和CEN全等，来得出结论．
点评：本题主要考查了等腰三角形的判定和全等三角形的判定与性质；通过已知和所求条件正确的构建出全等三角形是解题的关键．