
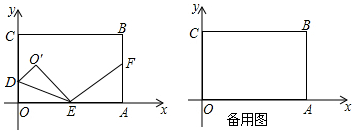
分析 (1)由题可得OE=3t,OD=t,BF=2t,易证四边形OABC是矩形,从而可得AB=OC=10,BC=OA=12,从而可求出OE、AF,即可得到点E、F的坐标;
(2)只需分两种情况(①△ODE∽△AEF,②△ODE∽△AFE)讨论,然后运用相似三角形的性质就可解决问题;
(3)过点O′作x轴的平行线与y轴交于点M,与过点E的y轴的平行线交于点N,如图1,易得△MDO′∽△NO′E,设MO′=a,根据相似三角形的性质可得到a与t的关系,从而将点O′的坐标用t的代数式表示,然后分两种情况(①DO′∥EF,如图2,②OF∥DE,如图3)讨论,然后运用相似三角形的性质就可解决问题.
解答 解:(1)由题可得OE=3t,OD=t,BF=2t.
∵BA⊥x轴,BC⊥y轴,∠AOC=90°,
∴∠AOC=∠BAO=∠BCO=90°,
∴四边形OABC是矩形,
∴AB=OC,BC=OA.
∵B(12,10),
∴BC=OA=12,AB=OC=10,
∴AF=10-2t,AE=12-3t,
∴点E的坐标为(3t,0),点F的坐标为(12,10-2t);
(2)①当△ODE∽△AEF时,
则有$\frac{OD}{AE}$=$\frac{OE}{AF}$,
∴$\frac{t}{12-3t}$=$\frac{3t}{10-2t}$,
解得t1=0(舍),t2=$\frac{26}{7}$;
②当△ODE∽△AFE时,
则有$\frac{OD}{AF}$=$\frac{OE}{AE}$,
∴$\frac{t}{10-2t}$=$\frac{3t}{12-3t}$,
解得t1=0(舍),t2=6.
∵点E运动到点A时,三点随之停止运动,
∴3t≤12,
∴t≤4.
∵6>4,∴t=6舍去,
综上所述:t的值为$\frac{26}{7}$;
(3)过点O′作x轴的平行线与y轴交于点M,与过点E的y轴的平行线交于点N,如图1,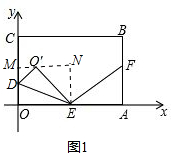
则有∠DMN=90°,∠N=90°.
由折叠可得DO′=DO=t,O′E=OE=3t,∠DO′E=∠DOE=90°,
∴∠DMO′=∠N=90°,∠MDO′=90°-∠MO′D=∠NO′E,
∴△MDO′∽△NO′E,
∴$\frac{MO′}{NE}$=$\frac{MD}{NO′}$=$\frac{O′D}{EO′}$=$\frac{t}{3t}$=$\frac{1}{3}$,
∴NE=3MO′,NO′=3MD.
设MO′=a,
则有OM=NE=3a,NO′=3t-a,MD=3a-t,
∴3t-a=3(3a-t),
解得:a=$\frac{3}{5}$t,
∴MO′=$\frac{3}{5}$t,OM=$\frac{9}{5}$t,
∴点O′的坐标为($\frac{3}{5}$t,$\frac{9}{5}$t).
①若DO′∥EF,如图2,
延长O′D交x轴于S,
则有O′M∥OS,∠DSE=∠FEA,
∴∠MO′D=∠DSE=∠FEA.
∵∠O′MD=∠EAF=90°,
∴△O′MD∽△EAF,
∴$\frac{MO′}{AE}$=$\frac{MD}{AF}$,
∴$\frac{\frac{3}{5}t}{12-3t}$=$\frac{\frac{9}{5}t-t}{10-2t}$,
解得:t1=0(舍去),t2=3;
②若OF∥DE,如图3,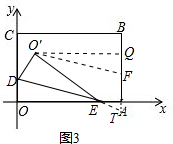
过点O′作x轴的平行线与AB交于点Q,延长DE交BA的延长线于点T,
同①可得△DOE∽△FQO′,
∴$\frac{OD}{QF}$=$\frac{OE}{QO′}$,
∴$\frac{t}{\frac{9}{5}t-(10-2t)}$=$\frac{3t}{12-\frac{3}{5}t}$,
解得t1=0(舍去),t2=$\frac{7}{2}$.
综上所述:t的值为3或$\frac{7}{2}$.
点评 本题主要考查了线相似三角形的判定与性质、矩形的判定与性质、轴对称的性质等知识,运用分类讨论的思想是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
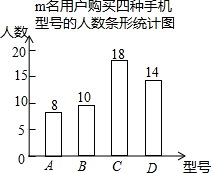 为了了解用户对某国手机的A、B、C、D四种型号的购买情况,某手机经销商随机对m名该手机用户的购买型号进行了调查,将调查数据整理并绘制成如图的统计图,根据统计图提供的信息,解答下列问题:
为了了解用户对某国手机的A、B、C、D四种型号的购买情况,某手机经销商随机对m名该手机用户的购买型号进行了调查,将调查数据整理并绘制成如图的统计图,根据统计图提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
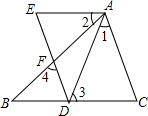 完成证明,说明理由.
完成证明,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
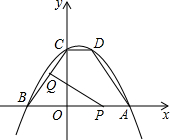 如图,抛物线y=ax2+bx+c经过点A(5,0),B(-3,0),C(0,4),过C作CD∥x轴交抛物线于D,连结BC、AD两个动点P、Q分别从A、B两点同时出发,都以每秒1个单位长度的速度运动,其中,点P沿着线段AB向B点运动,点Q沿着折线B→C→D的路线向D点运动,设这个两个动点运动的时间为t(秒)(0<t<7),△PQB的面积记为S.
如图,抛物线y=ax2+bx+c经过点A(5,0),B(-3,0),C(0,4),过C作CD∥x轴交抛物线于D,连结BC、AD两个动点P、Q分别从A、B两点同时出发,都以每秒1个单位长度的速度运动,其中,点P沿着线段AB向B点运动,点Q沿着折线B→C→D的路线向D点运动,设这个两个动点运动的时间为t(秒)(0<t<7),△PQB的面积记为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
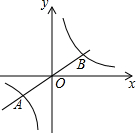 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$相交于A(-2,n)、B两点,则k的值为( )
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$相交于A(-2,n)、B两点,则k的值为( )| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
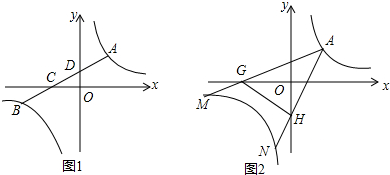
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com