
如图,已知A、B、C三点在⊙O上,∠A=50°,则∠BOC的度数为

A.50° B.25° C.75° D.100°
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源:2014-2015学年福建省九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列方程是关于x的一元二次方程的是( )
A.x2 +2y+1=0
B.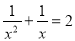
C.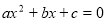
D.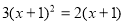
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省福安市小片区九年级上学期半期考试数学试卷(解析版) 题型:选择题
连接矩形各边中点得到的四边形是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市平谷区九年级上学期期末考试数学试卷(解析版) 题型:解答题
我区某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x (小时)变化的函数图象,其中BC段是双曲线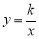 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:

(1)恒温系统在这天保持大棚内温度18℃的时间有 小时;
(2)求k的值;
(3)当x=16时,大棚内的温度约为 度.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市九年级上学期期中检测数学试卷(解析版) 题型:解答题
已知:⊙O是△ABC的外接圆,点M为⊙O上一点.
(1)如图,若△ABC为等边三角形,BM=1,CM=2,求AM的长;

小明在解决这个问题时采用的方法是:延长MC到E,使ME=AM,从而可证△AME为等边三角形,并且△ABM≌△ACE,进而就可求出线段AM的长.
请你借鉴小明的方法写出AM的长,并写出推理过程.
(2)若△ABC为等腰直角三角形,∠BAC=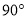 ,
,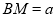 ,
, (其中
(其中 ),直接写出AM的长(用含有a,b的代数式表示).
),直接写出AM的长(用含有a,b的代数式表示).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市九年级上学期期中检测数学试卷(解析版) 题型:解答题
如图,△ABC的三个顶点 都在⊙O上,AP⊥BC于P,AM为⊙O的直径.
都在⊙O上,AP⊥BC于P,AM为⊙O的直径.
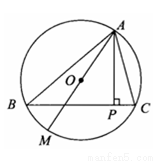
求证:∠BAM=∠CAP.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省淮北市五校九年级上学期第三次联考数学试卷(解析版) 题型:解答题
锐角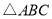 中,
中,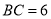 ,
,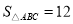 ,两动点
,两动点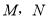 分别在边
分别在边 上滑动,且
上滑动,且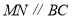 ,以
,以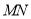 为边向下作正方形
为边向下作正方形 ,设其边长为
,设其边长为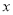 ,正方形
,正方形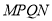 与
与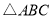 公共部分的面积为
公共部分的面积为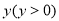 .
.
(1) 中边
中边 上高
上高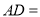 ;
;
(2)当 恰好落在边
恰好落在边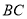 上(如图1);求正方形的边长
上(如图1);求正方形的边长
(3)当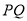 在
在 外部时(如图2),求
外部时(如图2),求 关于
关于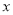 的函数关系式(写出
的函数关系式(写出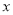 的取值范围),并求出
的取值范围),并求出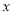 为何值时
为何值时 最大,最大值是多少?
最大,最大值是多少?

查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北沙河二十冶第3中学八年级上学期主科抽测数学卷(解析版) 题型:选择题
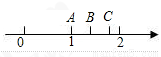
如图,数轴上A ,B两点表示的数分别为1和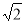 ,点A关于点B的对称点是点C,则点C所表示的数是( )
,点A关于点B的对称点是点C,则点C所表示的数是( )
A.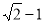 B.
B.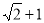 C.
C.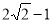 D.
D.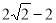
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com