
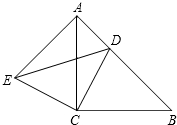
 如图,D为AB上一点,△ACE≌△BCD,AD2+DB2=DE2,试判断△ABC的形状,并说明理由.
如图,D为AB上一点,△ACE≌△BCD,AD2+DB2=DE2,试判断△ABC的形状,并说明理由. 分析 根据全等三角形的性质得出AC=BC,∠EAC=∠B,AE=BD,根据勾股定理的逆定理得出∠EAD=90°,求出∠ACB=90°,即可求出答案.
解答 解:△ABC是等腰直角三角形,
理由是:∵△ACE≌△BCD,
∴AC=BC,∠EAC=∠B,AE=BD,
∵AD2+DB2=DE2,
∴AD2+AE2=DE2,
∴∠EAD=90°,
∴∠EAC+∠DAC=90°,
∴∠DAC+∠B=90°,
∴∠ACB=180°-90°=90°,
∵AC=BC,
∴△ABC是等腰直角三角形.
点评 本题考查了全等三角形的性质定理和勾股定理的逆定理,能正确根据全等三角形的性质进行推理是解此题的关键,注意:全等三角形的对应角相等,对应边相等.


科目:初中数学 来源: 题型:解答题
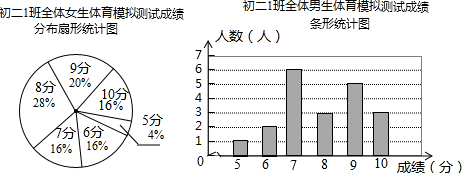
| 平均分 | 方差 | 中位数 | 众数 | |
| 男生 | 7.9 | 2 | 8 | 7 |
| 女生 | 7.92 | 1.99 | 8 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | -$\sqrt{13}$ | C. | 3$\sqrt{13}$ | D. | -3$\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
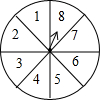 如图,转盘被平均分成8个区域,每个区域分别标注数字1、2、3、4、5、6、7、8,任意转动转盘一次,规定:如果指针恰好指在分割线上,那么重转一次,直到指针指向一个标有数字的区域为止.写出下列事件发生的概率:
如图,转盘被平均分成8个区域,每个区域分别标注数字1、2、3、4、5、6、7、8,任意转动转盘一次,规定:如果指针恰好指在分割线上,那么重转一次,直到指针指向一个标有数字的区域为止.写出下列事件发生的概率:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com