
【题目】四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.
(1)若点O在四边形ABCD的内部,
如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE=°;
(2)如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.
(3)如图3,若点O在四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.
【答案】
(1)125
(2)
解:(1)∠B+∠C+2∠DOE=360°,
理由:∵∠DOE=∠OAD+∠ADO,
∵AE、DO分别平分∠BAD、∠CDA,
∴2∠DOE=∠BAD+∠ADC,
∵∠B+∠C+∠BAD+∠ADC=360°,
∴∠B+∠C+2∠DOE=360°
(3)
解:∠B+∠C=2∠DOE,
理由:∵∠BAD+∠ADC=360°﹣∠B﹣∠C,∠EAD+∠ADO=180°﹣∠DOE,
∵AE、DO分别平分∠BAD、∠CDA,
∴∠BAD=2∠EAD,∠ADC=2∠ADO,
∴∠BAD+∠ADC=2(∠EAD+∠ADO),
∴360°﹣∠B﹣∠C=2(180°﹣∠DOE),
∴∠B+∠C=2∠DOE
【解析】解:(1)∵AD∥BC,∠B=40°,∠C=70°,
∴∠BAD=140°,∠ADC=110°,
∵AE、DO分别平分∠BAD、∠CDA,
∴∠BAE=70°,∠ODC=55°,
∴∠AEC=110°,
∴∠DOE=360°﹣110°﹣70°﹣55°=125°;
所以答案是:125;
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补),还要掌握多边形内角与外角(多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
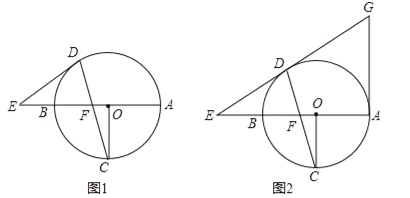
【题目】已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.
(1)如图1,求证:ED为⊙O的切线;
(2)如图2,直线ED与切线AG相交于G,且OF=1,⊙O的半径为3,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景 在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:
甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm.
乙组:如图2,测得学校旗杆的影长为900cm.
丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.

任务要求
(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;
(2)如图3,设太阳光线![]() 与
与![]() 相切于点
相切于点![]() .请根据甲、丙两组得到的信息,求景灯灯罩的半径(友情提示:如图3,景灯的影长等于线段
.请根据甲、丙两组得到的信息,求景灯灯罩的半径(友情提示:如图3,景灯的影长等于线段![]() 的影长;需要时可采用等式
的影长;需要时可采用等式![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批服装,每件进价为200元,由于换季滞销,商场决定将这种服装按标价的六折销售,若打折后每件服装仍能获利20%,则该服装标价是( )
A.350元
B.400元
C.450元
D.500元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,BD是△ABC的角平分线,P是射线AC上任意一点(不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交直线BD于E. 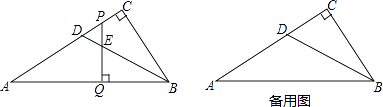
(1)如图,当点P在线段AC上时,说明∠PDE=∠PED.
(2)作∠CPQ的角平分线交直线AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点E、F分别在直线AB,CD上,点P在AB、CD之间,连结EP、FP,如图1,过FP上的点G作GH∥EP,交CD于点H,且∠1=∠2.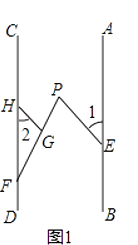
(1)求证:AB∥CD;
(2)如图2,将射线FC沿FP折叠,交PE于点J,若JK平分∠EJF,且JK∥AB,则∠BEP与∠EPF之间有何数量关系,并证明你的结论;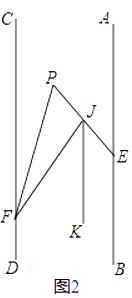
(3)如图3,将射线FC沿FP折叠,将射线EA沿EP折叠,折叠后的两射线交于点M,当EM⊥FM时,求∠EPF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com