练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在菱形ABCD中，E，F分别是BC，CD上的点，若△AEF是等边三角形，且EF=AB，则∠BAD的度数是（　　）
    A、100°B、105°
    C、110°D、120°
    考点：菱形的性质
    专题：
    分析：利用菱形以及等边三角形的性质用x表示出∠B和∠BAD，进而得出答案．
    解答：解：：如图所示：

    ∵在菱形ABCD中，E、F分别在BC、CD上，且△AEF是等边三角形，
    ∴AE=EF，
    ∵EF=AB，
    ∴AE=AB，
    ∴AB=AD=AE=AF，∠2=∠3=∠D=∠AFD，∠EAF=∠AEF=∠AFE=60°，
    设∠2=x，则∠2=∠3=∠D=∠AFD=x，
    故∠1=180°-2x，则∠DAF=180°-2x，
    ∵AD∥BC，
    ∴∠2+∠1+∠EAF+∠DAF=180°，
    ∴x+2（180°-2x）+60°=180°，
    解得：x=80°，
    则∠BAD=100°．
    故选A．
    点评：本题考查了菱形的性质，等边三角形的性质和判定的理解和运用，难度一般．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

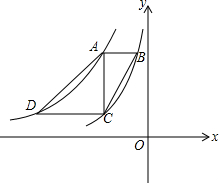    如图，是反比例函数y=-
    2
    x
    和y=-
    8
    x
    在第二象限中的图象，A是反比例函数y=-
    8
    x
    的图象上，且A点的横坐标为m（m＜0），AB．CD均平行于x轴，AC平行于y轴．   
    （1）用m表示A、B、C、D的坐标； 
    （2）求证：梯形ABCD的面积是定值； 
    （3）若△ABC和△ACD相似，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在Rt△ABC中，CD为斜边AB上的高，已知BC=4
    		3
    ，BD=4，那么tanA=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知抛物线y=x2-2和x轴交于A，B（点A在点B右边）两点，和y轴交于点C，P为抛物线上的动点．
    （1）求出A，C的坐标；
    （2）求动点P到原点O的距离的最小值，并求此时点P的坐标；
    （3）当点P在x轴下方的抛物线上运动时，过P的直线交x轴于E，若△POE和△POC全等，求此时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    小小的螺丝帽在日常生活中却有着很大的作用，常用的螺丝帽有六角螺丝和四角螺帽，请比较一下，制作同样厚度和宽度（指平行边间的距离）的这两种螺帽坯（如图），哪种用料少？两种螺帽毛坯用料的比例是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在Rt△ABC中，斜边AB的中垂线DE交BC于D，连接AD，若∠1：2=2：5，求∠B、∠BAC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

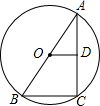    如图，AB是⊙O的直径，AC是弦，连接BC，若AB=10cm，BC=6cm，OD⊥AC于D，则AD的长为（　　）
    A、8cmB、6cm
    C、4cmD、2cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    二次函数y=-x2+4x+a的最大值是10，则a的值是（　　）
    A、4B、5C、6D、7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在平面直角坐标系中，规定把一个等边三角形先沿y轴翻折，再向上平移两个单位称为一次变换，如图，已知等边三角形ABC的顶点A、B、C的坐标分别是A（-2，-1-
    		3
    ），（-1，-1），（-3，-1），把等边三角形ABC经过连续2014次这样的变换得到等边三角形A′B′C′，则点A的对应点A′的坐标是
     
    ．

    查看答案和解析>>

    同步练习册答案