


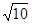 ,y=3x-12.
,y=3x-12.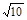
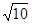


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、
、 分别在
分别在 轴、
轴、 轴的正半轴上,且
轴的正半轴上,且 ,点
,点 为线段
为线段 的中点.
的中点. 的长度为________________;
的长度为________________;
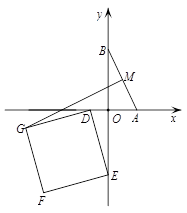
 为斜边作等腰直角三角形
为斜边作等腰直角三角形 ,当点
,当点 在第一象限时,求直线
在第一象限时,求直线 所对应的函数的解析式;
所对应的函数的解析式;
 、
、 分别在
分别在 轴、
轴、 轴的负半轴上,且
轴的负半轴上,且 ,以
,以 为边在第三象限内作正方形
为边在第三象限内作正方形 ,请求出线段
,请求出线段 长度的最大值,并直接写出此时直线
长度的最大值,并直接写出此时直线 所对应的函数的解析式.
所对应的函数的解析式.
|
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
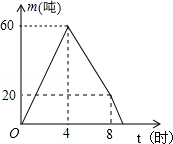
| A.8.4小时 | B.8.6小时 | C.8.8小时 | D.9小时 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com