Question

5．在平面直角坐标系xOy中，矩形AOBD的顶点A为（0，6$\sqrt{3}$），顶点B为（6，0），取OB、BD边上的中点分别记为点E、F，以BE，BF为边作矩形BEGF（如图1），将矩形BEGF绕点B旋转一周，在旋转过程中OE、DF所在直线交于点M．
（1）当矩形BEGF绕点B旋转到如图2时，求证：△OEB∽△DFB；
（2）当矩形BEGF绕点B旋转到60°时，
①求点M坐标；
②求点M在这个旋转过程中所经过的路径长；
（3）在矩形BEGF绕点B旋转一周的过程中，点E能否与点M重合？若能画出相应状态图，并求出点M坐标；若不能，请说明理由．

Answer 1

分析 （1）根据图1得：OB：BE=BD：BF=2：1，再利用同角的余角相等得∠OBE=∠DBF，则△OEB∽△DFB；
（2）①作辅助线，构建点M的运动路径，先求点C的坐标为（3，3$\sqrt{3}$），再证明△CDG是等边三角形，则有∠DCG=60°，所以∠DCM=∠DOB=60°，则CM∥OB，由等腰三角形三线合一得：CQ=QG=$\frac{1}{2}$OB=3，写出点M的坐标；
②如图4，点M在这个旋转过程中所经过的路径长就是$\widehat{BM}$的长，先计算圆心角∠BCM的度数，再利用弧长公式代入计算；
（3）画图发现是两种情况：点M分别为⊙C与⊙B的两个交点，圆C的方程为：（x-3）²+（y-3$\sqrt{3}$）²=36，圆B的方程为：（x-6）²+y²=9，列方程组，求解即可．

解答 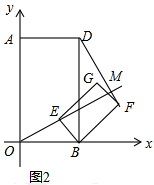证明：（1）根据图1知，E、F分别是OB、BD的中点，
∴图2中有：OB：BE=2：1，BD：BF=2：1，
∴OB：BE=BD：BF，
∵四边形APBD、ESFG都是矩形，
∴∠OBD=∠EBF=90°，
∴∠OBE=∠DBF，
∴△OEB∽△DFB；
（2）①如图3，由（1）知：∠BOM=∠BOE=∠BDF=∠BDM，
∴O、B、M、D四点共圆，且直径为OD，
∴∠OMD=∠OBD=90°，
∵∠EGF=90°，
∴D、G、F共线，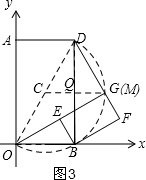
所以当矩形BEGF旋转时，点M在以BD为直径的圆上运动，
当旋转60°时，有∠OBE=60°，
∴BE=$\frac{1}{2}$OB=OB•cos60°=OB•cos∠OBE，
∴BE⊥OE，
∴∠BOE=30°，
∵BE⊥EG，
∴O、E、G三点共线，
∵A为（0，6$\sqrt{3}$），B为（6，0），
∴OB=6，BD=6$\sqrt{3}$，D（6，6$\sqrt{3}$），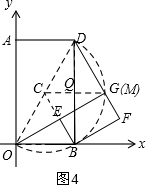
设C是OD的中点，则C（3，3$\sqrt{3}$），
∴tan∠ODB=$\frac{OB}{BD}$=$\frac{6}{6\sqrt{3}}$=$\frac{\sqrt{3}}{3}$，
∴∠ODB=30°，
∵∠BDF=∠BOE=30°，
∴∠ODM=∠ODB+∠BDG=60°，
∵△CDM是等腰三角形，
∴△CDM是等边三角形，
∴∠DCM=60°，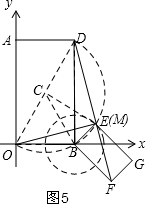
∴∠DCM=∠DOB=60°，
∴CM∥OB，
∴CQ=QG=$\frac{1}{2}$OB=3，
∴M（9，3$\sqrt{3}$）；
②如图4，连接BC，
由勾股定理得：OD=$\sqrt{{6}^{2}+（6\sqrt{3}）^{2}}$=12，
∴CD=$\frac{1}{2}$OD=6，
∠BCM=180°-∠DCM-∠OCB=60°，
矩形BEFG在开始旋转时，如图1，OE与DF交于点B，
如图2，旋转60°时，OE与DF交于点G，即在旋转过程中点M的运动路径为$\widehat{BM}$，
∴点M在这个旋转过程中所经过的路径长为：$\frac{60π•CD}{180}$=$\frac{6π}{3}$=2π；
（3）如图5和如图6，分两种情况，点M分别为圆C与以B为圆心，以BE=3为半径的圆B的两个交点，
圆C的方程为：（x-3）²+（y-3$\sqrt{3}$）²=36，
圆B的方程为：（x-6）²+y²=9，
两个方程相减得：2x-2$\sqrt{3}$y-9=0，
得x=$\sqrt{3}$y+$\frac{9}{2}$，代入圆B的方程消去x得：4y²-3$\sqrt{3}$y-$\frac{27}{4}$=0，
解得：y=$\frac{3\sqrt{3}±3\sqrt{15}}{8}$，对应的x=$\frac{45±9\sqrt{5}}{8}$，
所以当E、M重合时，点M的坐标为（$\frac{45+9\sqrt{5}}{8}$，$\frac{3\sqrt{3}+3\sqrt{15}}{8}$）或（$\frac{45-9\sqrt{5}}{8}$，$\frac{3\sqrt{3}-3\sqrt{15}}{8}$）．

点评 本题是相似形和旋转变换的综合题，难度较大，图形较为复杂；此题考查了利用四点共圆确定动点轨迹，并根据圆的方程求两圆交点坐标．