
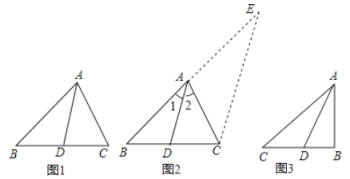
【题目】阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在△ABC中,AD平分∠BAC,则![]() =
=![]() .下面是这个定理的部分证明过程.
.下面是这个定理的部分证明过程.
证明:如图2,过C作CE∥DA.交BA的延长线于E.…
任务:(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知Rt△ABC中,AB=3,BC=4,∠ABC=90°,AD平分∠BAC,则△ABD的周长是 .
【答案】(1)见解析;(2)![]()
【解析】
(1)过C作CE∥DA.交BA的延长线于E,利用平行线分线段成比例定理得到![]() =
=![]() ,利用平行线的性质得∠2=∠ACE,∠1=∠E,由∠1=∠2得∠ACE=∠E,所以AE=AC,于是有
,利用平行线的性质得∠2=∠ACE,∠1=∠E,由∠1=∠2得∠ACE=∠E,所以AE=AC,于是有![]() =
=![]() ;
;
(2)先利用勾股定理计算出AC=5,再利用(1)中的结论得到![]() =
=![]() ,即
,即![]() =
=![]() ,则可计算出BD=
,则可计算出BD=![]() ,然后利用勾股定理计算出AD=
,然后利用勾股定理计算出AD=![]() ,从而可得到△ABD的周长.
,从而可得到△ABD的周长.
(1)过C作CE∥DA.交BA的延长线于E,
∵CE∥AD,
∴![]() =
=![]() ,∠2=∠ACE,∠1=∠E,
,∠2=∠ACE,∠1=∠E,
∵AD平分∠BAC
∴∠1=∠2,
∴∠ACE=∠E,
∴AE=AC,
∴![]() =
=![]() ;
;
(2)∵AB=3,BC=4,∠ABC=90°,
∴AC=5,
∵AD平分∠BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴BD=![]() ,
,
∴AD=![]() =
=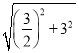 =
=![]() ,
,
∴△ABD的周长=![]() +3+
+3+![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2![]() ,则DB= ;
,则DB= ;
②当∠B= 度时,以O,D,E,C为顶点的四边形是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购买A型和B型课桌凳共200套,经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,,且购买4套A型和6套B型课桌凳共需1820元。
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
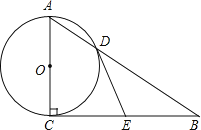
【题目】已知:![]() 是
是![]() 的角平分线,点
的角平分线,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,
,![]()
(1)如图1,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,若![]() 为等边三角形,在不添加辅助线的情况下,请你直接写出所有的全等三角形.
为等边三角形,在不添加辅助线的情况下,请你直接写出所有的全等三角形.
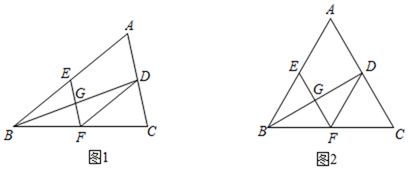
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15![]() .(sin15°=0.259,cos15°=0.966,tan15°=0.268,结果精确到0.1m)
.(sin15°=0.259,cos15°=0.966,tan15°=0.268,结果精确到0.1m)
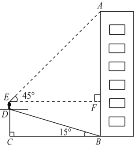
(1)求李华此时与地面的垂直距离CD的值;
(2)李华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45![]() ,求楼房AB的高度.
,求楼房AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在线段
在线段![]() 上,在
上,在![]() 的同侧作等腰
的同侧作等腰![]() 和等腰
和等腰![]() ,
,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() .对于下列结论:
.对于下列结论:
①![]() ;②
;②![]() ;③
;③![]() .其中正确的是( )
.其中正确的是( )
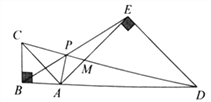
A. ①②③ B. ① C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
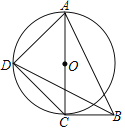
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径作⊙O,D为⊙O上一点,连接AD、BD、CD,且BD=AB
(1)求证:∠ABD=2∠BDC;
(2)若D为弧AC的中点,求tan∠BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
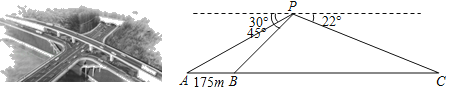
【题目】横卧于清波之上的黄石大桥与已经贯通的五峰山隧道将成为恩施城区跨越东西方向的最大直线通道,它把六角亭老城区与知名景点女儿城连为一体,缓解了恩施城区交通拥堵的现状.如图,某数学兴趣小组利用无人机在五峰山隧道正上空点P处测得黄石大桥西端点A的俯角为30°,东端点B(隧道西进口)的俯角为45°,隧道东出口C的俯角为22°,已知黄石大桥AB全长175米,隧道BC的长约多少米(计算结果精确到1米)?(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() 1.4,
1.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com