
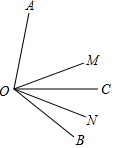
 如图,OM平分∠AOB,射线OC在∠BOM内部,ON是∠BOC的平分线.已知∠AOC=80°,那么∠MON的大小等于多少?
如图,OM平分∠AOB,射线OC在∠BOM内部,ON是∠BOC的平分线.已知∠AOC=80°,那么∠MON的大小等于多少? 分析 设∠CON=∠BON=x,∠MOC=y,则∠MOB=∠MOC+∠BOC=2x+y=∠AOM,∴∠AOC=∠AOM+∠MOC=2x+y+y=2(x+y)=80°.而∠MON=∠MOC+∠NOC=x+y,即可求解.
解答 解:∵ON平分∠BOC
∴∠CON=∠BON
设∠CON=∠BON=x,∠MOC=y
则∠MOB=∠MOC+∠BOC=2x+y
又∵OM平分∠AOB
∴∠AOM=∠BOM=2x+y
∴∠AOC=∠AOM+∠MOC=2x+y+y=2(x+y)
∵∠AOC=80°
∴2(x+y)=80°,
∴x+y=40°
∴∠MON=∠MOC+∠NOC=x+y=40°.
点评 此题考查的是角平分线的定义,主要利用了角平分线的定义和图中各角之间的和差关系,难度中等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
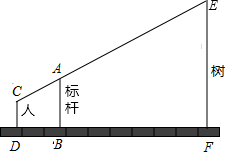 如图,竖立在点B处的标杆AB 长2.1米,某测量工作人员站在D点处,此时人眼睛C与标杆顶端A、树顶端E在同一直线上(点D、B、F也在同一直线上),已知此人眼睛与地面的距离CD 长1.6米,且BD=1米,BF=5米,求所测量树的高度.
如图,竖立在点B处的标杆AB 长2.1米,某测量工作人员站在D点处,此时人眼睛C与标杆顶端A、树顶端E在同一直线上(点D、B、F也在同一直线上),已知此人眼睛与地面的距离CD 长1.6米,且BD=1米,BF=5米,求所测量树的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
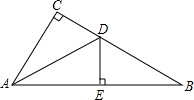 如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB.
如图,在直角△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com