
 如图,某天晚8点时,一台风中心位于点O正北方向160千米点A处,台风中心以每小时20千米的速度向东南方向移动,在距台风中心小于等于120千米的范围内将受到台风影响,同时在点O有一辆汽车以每小时40千米的速度向东行驶.
如图,某天晚8点时,一台风中心位于点O正北方向160千米点A处,台风中心以每小时20千米的速度向东南方向移动,在距台风中心小于等于120千米的范围内将受到台风影响,同时在点O有一辆汽车以每小时40千米的速度向东行驶.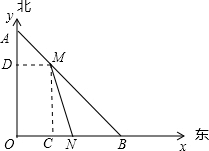
 AM=10
AM=10 t,
t, t,160-10
t,160-10 t),
t), t)2+(160-10
t)2+(160-10 t)2=1202,
t)2=1202, )t2-32
)t2-32 t+112=0,
t+112=0, -6912<0,
-6912<0,

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com