解:(1)∵四边形ABCD是正方形,
∴AD=DC,∠ADC=90°,
即A绕D旋转到C点,
∴旋转中心是点D,旋转角度是90°,
∠EDF=∠ADC=90°,DE=DF,
∴△DEF是等腰直角三角形,
故答案为:点D,90°,等腰直角;
(2)①依题意,得:△ADE≌△BAH≌△CDF,
∴∠BAH=∠ADE,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠BAH+∠GAD=90°,
∴∠ADE+∠GAD=90°,
∴∠AGD=90°,
∴AH⊥DE;
②在Rt△ADE中,根据勾股定理,得:
DE=
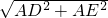
=

=10,
∵S
△ADE=

×AD×AE=

×DE×AG,
∴DE×AG=AD×AE,
∴8×6=10×AG,
AG=4.8.
分析:(1)根据正方形性质得出AD=DC,∠ADC=90°,根据已知△DAE经过逆时针旋转后到达△DCF的位置即可得出旋转中心和旋转角度,根据旋转性质求出DE=DF,即可得出△DEF是等腰直角三角形;
(2)①根据旋转性质得出△ADE≌△BAH≌△CDF,推出∠BAH=∠ADE,根据正方形性质推出∠ADE+∠GAD=90°,求出∠AGD=90°,即可得出答案;②根据勾股定理求出DE,根据三角形的面积公式得出DE×AG=AD×AE,代入求出即可.
点评:本题考查了正方形性质,勾股定理,三角形的面积,旋转的性质,三角形的内角和定理等知识点,主要考查学生综合运用定理进行推理和计算的能力,题目比较好,有一定的难度.

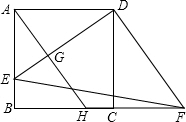
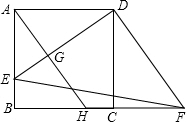 如图,已知正方形ABCD的边长是8,E是AB边上的点,且AE=6,△DAE经过逆时针旋转后到达△DCF的位置.
如图,已知正方形ABCD的边长是8,E是AB边上的点,且AE=6,△DAE经过逆时针旋转后到达△DCF的位置.
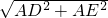 =
= =10,
=10, ×AD×AE=
×AD×AE= ×DE×AG,
×DE×AG,

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案 (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上. 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.