
����Ŀ��2019�����й�����70���꣬��Ϊ��ʱ�ڵ������꣬����Ӧ�ü縺��ʵ�ִֹ�ΰ���˵����Σ�Ϊ������ѧ���İ��������黳����Уѧ������ʦ��5����Ѯ����˳�ȥ����ս���������ѧ����֪ѧ������������ʦ������12����20�ˣ�ѧ������ʦ��������540�ˣ�
��1�������ȥ����ս���������ѧ��ѧ������ʦ���������Ƕ��٣�
��2�����ѧУ������A�ͳ���B�ͳ���14��������B�ͳ����7��������֪A�ͳ�ÿ����������35�ˣ������Ϊ2000Ԫ��B�ͳ�ÿ����������45�ˣ������Ϊ3000Ԫ���������õ��������
���𰸡���1��ȥ����ս���������ѧ��ѧ����500�ˣ���ʦ��40�ˣ���2����õ�����������Ϊ������A�ʹ�ͳ�9��������B�ʹ�ͳ�5����
��������
��1����ȥȥ����ս���������ѧ��ѧ����x�ˣ���ʦ��y�ˣ�������ѧ������������ʦ������12����20�ˣ�ѧ������ʦ��������540�����г������飬Ȼ����ⷽ���鼴�ɣ�
��2��������B�ʹ�ͳ�m����������A�ʹ�ͳ���14��m����������������B�ͳ����7������������������С�����������г�����m�IJ���ʽ�飬���õ�m��ȡֵ��Χ��mȡ�������ٸ�������õ������������m�Ĺ�ϵ��Ȼ��ȡ��Сֵ����.
�⣺��1����ȥȥ����ս���������ѧ��ѧ����x�ˣ���ʦ��y�ˣ�
�����⣬�ã�
![]() ��
��
��ã�![]() ��
��
��ȥ����ս���������ѧ��ѧ����500�ˣ���ʦ��40�ˣ�
��2��������B�ʹ�ͳ�m����������A�ʹ�ͳ���14��m������
�����⣬�ã�
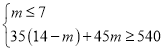 ��
��
��ã�5��m��7��
��m��������
��m��5��6��7��
�����������ΪwԪ�������⣬�ã�
w��3000m+2000��14��m����1000m+28000��
��1000��0��
��w��ֵ��mֵ�����������
����m��5ʱ��wȡ����Сֵ��
����õ�����������Ϊ������A�ʹ�ͳ�9��������B�ʹ�ͳ�5����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����κ���y=ax2+bx+c��ͼ����ͼ��ʾ��OA=OC�����������ߵ�����д�����º���a��b��c������ĸ�ĵ�ʽ��ʽ����![]() =-1����ac+b+1=0����abc>0����a-b+c>0.��ȷ�������______________.
=-1����ac+b+1=0����abc>0����a-b+c>0.��ȷ�������______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η���
��һԪ���η���![]() ��
��
��1�����˷��̵�һ����Ϊ1����![]() ��ֵ��
��ֵ��
��2����֤������![]() ȡ��ʵ�����˷��̶�����������ȵ�ʵ������
ȡ��ʵ�����˷��̶�����������ȵ�ʵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
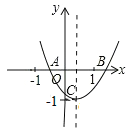
����Ŀ����ͼ����13��7�������У�ÿ��С�����α߳�����1���䶥�������㣬��ͼA��B��D��E��M��P��Ϊ��㣮
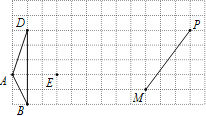
��1�����������л���ABCD��Ҫ��C���ڸ���ϣ�
��2���ڣ�1������ABCD�Ҳ�����EFG����ʹEF=5��FG=3��EG=![]() ��
��
��3����MPΪ�Խ�������MNPQ��M��N��P��Q����ʱ�뷽�����У���ʹ����MNPQ�����Ϊ10��
��4����ֱ��AE����һ��W��ʹWB��WM��ֵ��С���������СֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��BAD����BCE��Ϊ����ֱ�������Σ���BAD=��BCE=90������MΪDE���е㣬����E��ADƽ�е�ֱ�߽�����AM�ڵ�N��
��1����A��B��C������ͬһֱ����ʱ����ͼ1����ֱ��д���߶�AD��NE��������ϵΪ�� ����
��2����ͼ1�е���BCE�Ƶ�B��ת����A��B��E������ͬһֱ����ʱ����ͼ2�����ж���ACN��ʲô���������β�˵�����ɣ�
��3����ͼ1����BCE�Ƶ�B��ת��ͼ3λ�ã���ʱA��B��M������ͬһֱ���ϣ���AC=3![]() ��AD=1�����ı���ACEN�����Ϊ�� ����
��AD=1�����ı���ACEN�����Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
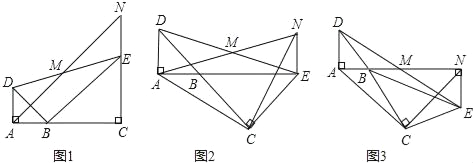
����Ŀ����ͼ����������ABCD�У��߳�Ϊa����O�ǶԽ���AC���е㣬��E��BC���ϵ�һ�����㣬OE��OF��AB���ڵ�F����G��H�ֱ��ǵ�E��F����ֱ��AC�ĶԳƵ㣬��E�ӵ�C�˶�����Bʱ����ͼ����Ӱ���ֵ������___________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͨѶ������Ѹ�ͷ�չ��������֮��Ĺ�ͨ��ʽ����������ݣ�ijУ��ѧ��ȤС�������������ϲ���Ĺ�ͨ��ʽ�������ʾ���ÿ�˱�ѡ��ֻѡһ�֣�����ȫУ��Χ����������˲���ѧ������ͳ�ƽ������������������������ͳ��ͼ������ͼ����������Ϣ�������������
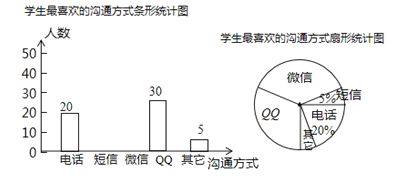
��1�����ͳ�ƹ������________��ѧ����������ͳ��ͼ������ʾ��QQ��������Բ�ĽǵĶ���Ϊ___________��
��2���뽫����ͳ��ͼ����������
��3��ij��ס�������ͬѧ���������������QQ�������绰�����ֹ�ͨ��ʽ��ѡһ�ַ�ʽ��Է���ϵ�������б�����״ͼ�ķ�������ס�������ͬѧǡ��ѡ��ͬһ�ֹ�ͨ��ʽ�ĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��������װ�к졢�ơ���������ɫ��ƹ������ɫ���������ͬ�������а������1������������������һ�����ǰ���ĸ�����![]() ��
��
��1�������к���ĸ�����
��2���ȴӰ�������������һ���������ɫ��Żأ��ٴӰ�������������һ��������������������ɫ��ͬ�ĸ��ʣ�������ͼ���б�����⣩��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAD=��CAE=90�㣬AB=AD��AE=AC��AF��CB������ΪF��
��1����֤����ABC�ա�ADE��
��2������FAE�Ķ�����
��3����֤��CD=2BF+DE��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com