
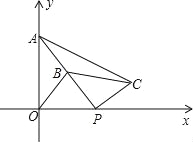
【题目】如图,在平面直角坐标系中,点A的坐标为(0,2),点P(t,0)在x轴上,B是线段PA的中点.将线段PB绕着点P顺时针方向旋转90°,得到线段PC,连结OB、BC.
(1)判断△PBC的形状,并简要说明理由;
(2)当t>0时,试问:以P、O、B、C为顶点的四边形能否为平行四边形?若能,求出相应的t的值?若不能,请说明理由;
(3)当t为何值时,△AOP与△APC相似?
【答案】(1)等腰直角三角形(2)t=2(3)±1或±4
【解析】
试题分析:(1)根据旋转的现在得出PB=PC,再根据B是线段PA的中点,得出∠BPC=90°,从而得出△PBC是等腰直角三角形.
(2)根据∠OBP=∠BPC=90°,得出OB∥PC,再根据B是PA的中点,得出四边形POBC是平行四边形,当OB⊥BP时,得出OP2=2OB2,即t2=2(![]() t2+1),求出符合题意的t的值,即可得出答案;
t2+1),求出符合题意的t的值,即可得出答案;
(3)根据题意得出∠AOP=∠APC=90°,再分两种情况讨论,当![]() 时和
时和![]() 时,得出△AOP∽△APC和△AOP∽△CPA,分别求出t的值即可.
时,得出△AOP∽△APC和△AOP∽△CPA,分别求出t的值即可.
试题解析:(1)△PBC是等腰直角三角形,理由如下:
∵线段PB绕着点P顺时针方向旋转90°,得到线段PC,
∴PB=PC,
∵B是线段PA的中点,
∴∠BPC=90°,
∴△PBC是等腰直角三角形.
(2)当OB⊥BP时,以P、O、B、C为顶点的四边形为平行四边形.
∵∠OBP=∠BPC=90°,
∴OB∥PC,
∵B是PA的中点,
∴OB=![]() AP=BP=PC,
AP=BP=PC,
∴四边形POBC是平行四边形,
当OB⊥BP时,有OP=![]() OB,即OP2=2OB2,
OB,即OP2=2OB2,
∴t2=2(![]() t2+1),
t2+1),
∴t1=2,t2=﹣2(不合题意),
∴当t=2时,以P、O、B、C为顶点的四边形为平行四边形.
(3)由题意可知,∠AOP=∠APC=90°,
当![]() 时,
时,
△AOP∽△APC,
此时OP=![]() OA=1,
OA=1,
∴t=±1,
当![]() 时,
时,
△AOP∽△CPA,
此时OP=2OA=4,
∴t=±4,
∴当t=±1或±4时,△AOP与△CPA相似.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:

(1)农民自带的零钱是多少?
(2)降价前每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?
(4)请问这个水果贩子一共赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知开始输入的x的值为正整数.若最后输出的结果为144,则满足条件的x的值为________;若经过一次运算就能输出结果,则x的最小值为________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小丽做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当实验次数为10000次时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如由你摸球一次,你摸到白球的概率P(摸到白球)= ;
(3)盒子中有黑球 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
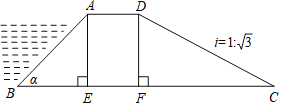
【题目】如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=![]() 米,背水坡CD的坡度i=1:
米,背水坡CD的坡度i=1: ![]() (i为DF与FC的比值),则背水坡CD的坡长为_______米.
(i为DF与FC的比值),则背水坡CD的坡长为_______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求解一元二次方程
(1)4x2﹣8x+1=0(配方法) (2)7x(5x+2)=6(5x+2)(因式分解法)
(3)3x2+5(2x+1)=0(公式法) (4)x2﹣2x﹣8=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)根据下列叙述填依据:
已知:如图①,AB∥CD,∠B+∠BFE=180°,求∠B+∠BFD+∠D的度数.
解:因为∠B+∠BFE=180°,
所以AB∥EF( ).
又因为AB∥CD,
所以CD∥EF( ).
所以∠CDF+∠DFE=180°( ).
所以∠B+∠BFD+∠D=∠B+∠BFE+∠DFE+∠D=360°.
(2)根据以上解答进行探索:如图②,AB∥EF,∠BDF与∠B,∠F有何数量关系?并说明理由.
(3)如图③④,AB∥EF,你能探索出图③、图④两个图形中,∠BDF与∠B,∠F的数量关系吗?请直接写出结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
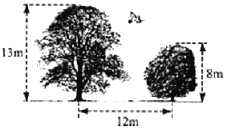
【题目】如图,有一只小鸟在一棵高13m的大树树梢上捉虫子,它的伙伴在离该树12m,高8m的一棵小树树梢上发出友好的叫声,它立刻以2m/s的速度飞向小树树梢,它最短要飞多远?这只小鸟至少几秒才可能到达小树和伙伴在一起?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com