

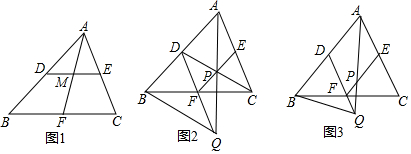
���� ��1������֪�ó���DAC=��CAB=30�㣬���������ڽǺͶ����ó���D+��ACD=150�㣬�ɡ�BCD=��ACD+��ACB=150�㣬�ó���D=��ACB��֤����ADC�ס�ACB���ó���Ӧ�߳ɱ������ó�AC2=AB•AD�����ɵó����ۣ�
��2������֪������֤�á�ADC�ס�ACB���ó�D=��ACB��������֪�������������ڽǺͶ����ó���DAC+2��DAC=180�㣬�����DA=60�㣬���ɵó���DAB�Ķ�����
��3�����ݡ��ɷ��ı��Ρ��Ķ������AB•AD�����㼴�ɣ�
��� ��1��֤�����ߡ�DAB=60�㣬ACƽ�֡�DAB��
���DAC=��CAB=30�㣬
���D+��ACD=180��-30��=150�㣬
�ߡ�BCD=��ACD+��ACB=150�㣬
���D=��ACB��
���ADC�ס�ACB��
��AD��AC=AC��AB��
��AC2=AB•AD��
���ı���ABCDΪ���ɷ��ı��Ρ���
��2���⣺��ACƽ�֡�DAB��
���DAC=��BAC��
��AC2=AB•AD��
��AD��AC=AC��AB��
���ADC�ס�ACB��
���D=��ACB��
�ߡ�DCB=��DAB��
���DCB=��DCA+��ACB=2��DAC��
�ߡ�DAC+��D+��ACB=180�㣬
���DAC+2��DAC=180�㣬
��ã���DAC=60�㣬
���DAB=120�㣻
��3�����ı���ABCDΪ���ɷ��ı��Ρ���AC=4��
��AB•AD=AC2=16��
��DA��DBʱ����DAB�����������Ϊ8��
�ʴ�Ϊ��8��
���� �������������ۺ���Ŀ�����������������ε��ж������ʡ��������ڽǺͶ��������ɶ������¶����ı��ε�֪ʶ�����������¶����ı��Σ�֤�������������ǽ������Ĺؼ���


 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �ڢ� | C�� | �ڢ� | D�� | �ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=$\frac{1}{2}$x+2 | B�� | y=2x+4 | C�� | y=-2x+2 | D�� | y=-$\frac{1}{2}$x+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{1-\sqrt{3}}{2}$ | C�� | $\frac{1+\sqrt{3}}{2}$ | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com