
����Ŀ����ͼ1����Rt��ABC�У���C=90�㣬AC=6��BC=8������P�ӵ�A��ʼ�ر�AC���C��1����λ���ȵ��ٶ��˶�������Q�ӵ�C��ʼ�ر�CB���B��ÿ��2����λ���ȵ��ٶ��˶�������P��PD//BC����AB�ڵ�D������PQ�ֱ�ӵ�A��Cͬʱ������������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����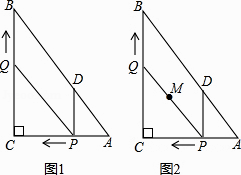
��1��ֱ���ú�t�Ĵ���ʽ�ֱ��ʾ��QB= �� PD= ��
��2���Ƿ����t��ֵ��ʹ�ı���PDBQΪ���Σ������ڣ����t��ֵ���������ڣ�˵�����ɣ���̽����θı�Q���ٶȣ������˶�����ʹ�ı���PDBQ��ijһʱ��Ϊ���Σ����Q���ٶȣ�
��3����ͼ2���������˶������У�����߶�PQ�е�M��������·������
���𰸡�
��1��8��2t��![]()
t
��2��
�⣺������
��Rt��ABC�У���C=90�㣬AC=6��BC=8��
��AB=10
��PD//BC��
���APD�ס�ACB��
�� ![]() ����
���� ![]() ��
��
��AD= ![]() t��
t��
��BD=AB��AD=10�� ![]() t��
t��
��BQ//DP��
�൱BQ=DPʱ���ı���PDBQ��ƽ���ı��Σ�
��8��2t= ![]() ����ã�t=
����ã�t= ![]() ��
��
��t= ![]() ʱ��PD=
ʱ��PD= ![]() =
= ![]() ��BD=10��
��BD=10�� ![]() ��
�� ![]() =6��
=6��
��DP��BD��
��PDBQ��������
���Q���ٶ�Ϊÿ��v����λ���ȣ�
��BQ=8��vt��PD= ![]() t��BD=10��
t��BD=10�� ![]() t��
t��
Ҫʹ�ı���PDBQΪ���Σ���PD=BD=BQ��
��PD=BDʱ���� ![]() t=10��
t=10�� ![]() t����ã�t=
t����ã�t= ![]()
��PD=BQ��t= ![]() ʱ����
ʱ���� ![]() =8��
=8�� ![]() ����ã�v=
����ã�v= ![]()
����Q���ٶ�Ϊÿ�� ![]() ����λ����ʱ������
����λ����ʱ������ ![]() �룬�ı���PDBQ������
�룬�ı���PDBQ������
��3��
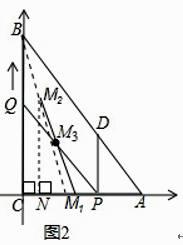
�⣺��ͼ2����CΪԭ�㣬��AC���ڵ�ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵ��
�����⣬��֪0��t��4����t=0ʱ����M1������Ϊ��3��0������t=4ʱ��M2������Ϊ��1��4����
��ֱ��M1M2�Ľ���ʽΪy=kx+b��
�� ![]() ��
��
��� ![]() ��
��
��ֱ��M1M2�Ľ���ʽΪy=��2x+6��
�ߵ�Q��0��2t����P��6��t��0��
�����˶������У��߶�PQ�е�M3�����꣨ ![]() ��t����
��t����
��x= ![]() ����y=��2x+6��y=��2��
����y=��2x+6��y=��2�� ![]() +6=t��
+6=t��
���M3��ֱ��M1M2�ϣ�
����M2��M2N��x���ڵ�N����M2N=4��M1N=2��
��M1M2=2 ![]()
���߶�PQ�е�M��������·����Ϊ2 ![]() ��λ���ȣ�
��λ���ȣ�
���������⣺��1����������ã�CQ=2t��PA=t��
��QB=8��2t��
����Rt��ABC�У���C=90�㣬AC=6��BC=8��PD//BC��
���APD=90�㣬
��tanA= ![]() =
= ![]() ��
��
��PD= ![]() t��
t��
���Դ��ǣ���1��8��2t�� ![]() t��
t��
�����㾫����������Ҫ���������ε����ʺ����������ε�Ӧ�õ����֪ʶ�㣬��Ҫ�������ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�룻��ߣ��������ܵ��ﶥ��������ĸ߶ȣ�ͨ���á���ͬһʱ�������Ӱ���ɱ�������ԭ���������ࣺ�������ܵ��������ľ�����������������������������ȷ�����⣮


 �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
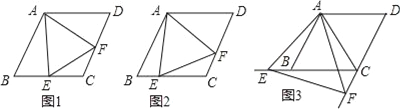
����Ŀ����֪�ı���ABCD�����Σ�AB=4����ABC=60�㣬��EAF�����߷ֱ�������CB��DC�ཻ�ڵ�E��F���ҡ�EAF=60�㣮
��1����ͼ1������E���߶�CB���е�ʱ��ֱ��д���߶�AE��EF��AF֮���������ϵΪ�� ��
��2����ͼ2������E���߶�CB������һ��ʱ����E����B��C�غϣ�����֤��BE=CF��
��3������AEF�ܳ�����Сֵ��
(4) ��ͼ3������E���߶�CB���ӳ����ϣ��ҡ�EAB=15��ʱ�����F��BC�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=x2+bx+c��x��ֻ��һ������M����ƽ����x���ֱ��l����A��B���㣬��AB=3�����M��ֱ��l�ľ���Ϊ�� �� 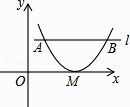
A.![]()
B.![]()
C.2
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
С�����о���ѧ����ʱ����һ�����壺�����ź�˳����������� ![]() ����Ϊ����
��������![]() .����
.����![]() ��
�� ![]() ��
�� ![]() ��������������Сֵ��Ϊ����
��������������Сֵ��Ϊ����![]() �ļ�ֵ�����磬��������2����1��3����Ϊ
�ļ�ֵ�����磬��������2����1��3����Ϊ![]() ��
�� ![]() ��
�� ![]() ����������2����1��3�ļ�ֵΪ
����������2����1��3�ļ�ֵΪ![]() ��
��
С����һ�����֣����ı�����������˳��ʱ�����õ������ж�����������������������Ӧ�ļ�ֵ�������Щ�1��2��3�ļ�ֵΪ![]() ������3����1��2�ļ�ֵΪ1�����������о���С�����֣�������2����1��3���������������ղ�ͬ������˳��õ��IJ�ͬ�����У���ֵ����СֵΪ
������3����1��2�ļ�ֵΪ1�����������о���С�����֣�������2����1��3���������������ղ�ͬ������˳��õ��IJ�ͬ�����У���ֵ����СֵΪ![]() ���������ϲ��ϣ��ش��������⣺
���������ϲ��ϣ��ش��������⣺
��1�����Щ�4����3��2�ļ�ֵΪ ��
��2��������4����3��2�������������ղ�ͬ��˳�����У��ɵõ����ɸ����У���Щ���еļ�ֵ����СֵΪ ��ȡ�ü�ֵ��Сֵ������Ϊ ��д��һ�����ɣ���
��3����2����9��a��a��1�������������ղ�ͬ��˳�����У��ɵõ����ɸ����У�����Щ���еļ�ֵ����СֵΪ1����a��ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=kx+b��ͼ����A(1,1)�͵�B(1,3).��
(1)��һ�κ����ı���ʽ��
(2)��ֱ��AB��������Χ�ɵ������ε������
(3)����x�����ҵ�һ��P��ʹ��PA+PB��С�������P������.
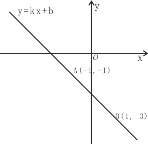
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬѧ�Ƕ�֪����|5������2��|��ʾ5�멁2֮��ľ���ֵ��ʵ����Ҳ������Ϊ5�멁2���������������Ե�����֮��ľ��룮��̽����
��1����|5������2��|=________��
��2�������ϱ�ʾx�ͩ�1������֮��ľ����ʾΪ________��
��3���ҳ����з�������������x��ʹ|x+5|+|x��2|=7��������������________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ù����Σ���ʦ�ںڰ���д����������ʽ![]() ��
��![]() ���ô���֮��������������ʽ���⿼�Է���
���ô���֮��������������ʽ���⿼�Է���
��1��С����С�������Ϊ��������ʽ![]() ��
��![]() ��ֵ��1����3a2��2��2a2+a��+2��a2��3a����ֵ��
��ֵ��1����3a2��2��2a2+a��+2��a2��3a����ֵ��
��2��С����Ϊ��һ��С��������С��������Ϊ����֪aΪ�������Ƚϴ���ʽ![]() ��
��![]() �Ĵ�С�������С���������
�Ĵ�С�������С���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ǽס�������˾���������������������ͳ��ͼ������ͳ��ͼ�ó����н��ۣ�������ȷ���ǣ� ��
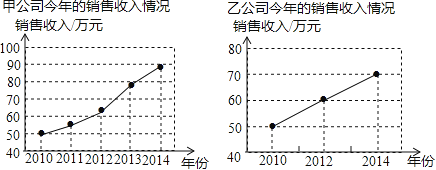
A����˾������������������ٶȱ��ҹ�˾��
B���ҹ�˾������������������ٶȱȼ�˾��
C���ס�������˾������������������ٶ�һ����
D������ȷ���ס�������˾�����������������ٶȵĿ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ֱ������ABCD ��ֱ��DC����ƽ�ƿɵ�ֱ������HFGE�����AB��4��BC��9��BI��1.2��HI��3��ô��Ӱ���Ϊ_________��
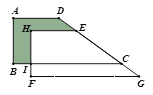
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com