
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=![]() ,BC=1.连结BF,分别交AC、DC、DE于点P、Q、R.
,BC=1.连结BF,分别交AC、DC、DE于点P、Q、R.
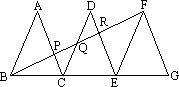
(1)求证:△BFG∽△FEG,并求出BF的长;
(2)观察图形,请你提出一个与点P相关的问题,并进行解答(根据提出问题的层次和解答过程评分).
|
(1)证明:∵△ABC≌△DCE≌△FEG,∴BC=CE=EG= (2)A层问题(较浅显的,仅用到了1个知识点).例如:①求证:∠PCB=∠R EC.(或问∠PCB与∠REC是否相等?)等;②求证:PC∥RE.(或问线段PC与RE是否平行?)等.B层问题(有一定思考的,用到了2~3个知识点).例如:①求证:∠BPC=∠BFG等,求证:BP=PR等;②求证:△ABP∽△CQP等,求证:△BPC∽△BRE等;③求证:△ABP∽△DQR等;④求BP∶PF的值等.C层问题(有深刻思考的,用到了4个或4个以上知识点、或用到了(1)中结论).例如:①求证:△ABP≌△ERF;②求证:PQ=RQ等;③求证:△BPC是等腰三角形;④求证:△PCQ≌△RDQ等;⑤求AP∶PC的值等;⑥求BP的长;⑦求证:PC=
A层解答举例.求证:PC∥RE.证明:∵△ABC≌△DCE,∴∠PCB=∠REB,∴PC∥RE.B层解答举例.求证:BP=PR.证明∵∠ACB=∠REC,∴AC∥DE.又∵BC=CE,∴BP=PR.C层解答举例.求AP∶PC的值.解:AC∥FG,∵ |


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 24、如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH.
24、如图,已知△ABC和△CDE均为等边三角形,且点B、C、D在同一条直线上,连接AD、BE,交CE和AC分别于G、H点,连接GH.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.
如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.查看答案和解析>>
科目:初中数学 来源: 题型:
 17、(1)已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h(要求尺规作图,不写作法和证明)
17、(1)已知线段a,h,用直尺和圆规作等腰三角形ABC,底边BC=a,BC边上的高为h(要求尺规作图,不写作法和证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com