
【题目】“十一”黄金周期间,某动物园在![]() 天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 (单位:万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若![]() 月
月![]() 日的游客人数记为
日的游客人数记为![]() 万人,请用含
万人,请用含![]() 的代数式表示
的代数式表示![]() 月
月![]() 日的游客人数,并直接写出七天内游客人数最多的是哪一天?
日的游客人数,并直接写出七天内游客人数最多的是哪一天?
(2)若![]() 月
月![]() 日的游客人数为
日的游客人数为![]() 万人,门票每人
万人,门票每人![]() 元,问黄金周期间该动物园门票总收入是多少万元?
元,问黄金周期间该动物园门票总收入是多少万元?
【答案】(1)(a+2.4)万人;![]() 月
月![]() 日人最多;(2)408万元
日人最多;(2)408万元
【解析】
(1)9月30日的游客人数为a万人,10月1日的游客人数是(a+1.6)万人,10月2日的游客人数是(a+1.6+0.8)万人;用含a的代数式表示出每天的游客人数,然后比较可得到结果;
(2)先计算出游客总数,再计算黄金周期间动物园的门票收入.
解:(1)10月2日游客人数是:a+1.6+0.8=a+2.4(万人);
∵七天内游客人数分别是(单位:万人):10月1日:a+1.6,10月2日:a+2.4,10月3日:a+2.8,10月4日:a+2.4,10月5日:a+1.6,10月6日:a+1.8,10月7日:a+0.6.
∵a+2.8最大,∴10月3日游客人数最多.
答:10月2日游客人数是(a+2.4)万人;10月3日游客人数最多.
(2)七天游客总人数为:(a+1.6)+(a+2.4)+(a+2.8)+(a+2.4)+(a+1.6)+(a+1.8)+(a+0.6)=7a+13.2,
当a=2时,原式=27.2,
∴27.2×15=408(万元).
答:黄金周期间该公园门票收入是408万元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A,B,C,D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A,D两点表示的数分别为-5和6,点E为BD的中点,在数轴上的整数点中,离点E最近的点表示的数是( )
![]()
A.2B.1
C.0D.-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,两个完全相同的三角形纸片 ABC 和 DEC 重合放置,其中∠C=90°,∠B=∠E=30°.
⑴ 操作发现:如图 2,固定△ABC,使△DEC 绕点 C 旋转,当点 D 恰好落在 AB 边上时, 填空:
①线段 DE 与 AC 的位置关系是 ;
②设△BDC 的面积为 S1,△AEC 的面积为 S2,则 S1 与 S2 的数量关系是 .
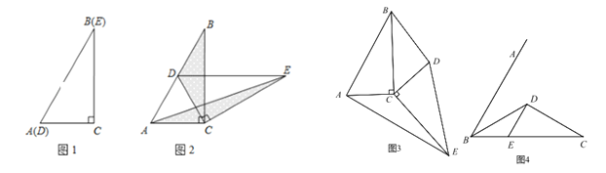
⑵ 猜想论证
当△DEC 绕点 C 旋转到如图 3 所示的位置时,请猜想(1)中 S1 与 S2 的数量关系是否仍 然成立?若成立,请证明;若不成立,请说明理由.
⑶ 拓展探究
已知∠ABC=60°,BD 平分∠ABC,BD=CD,BE=6,DE∥AB 交 BC 于点 E(如图 4).若在射线 BA 上存在点 F,使 S△DCF=S△BDE,请求相应的 BF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
某些代数恒等式可用一些卡片拼成的图形的面积来解释.例如,图①可以解释![]() ,因此,我们可以利用这种方法对某些多项式进行因式分解.
,因此,我们可以利用这种方法对某些多项式进行因式分解.
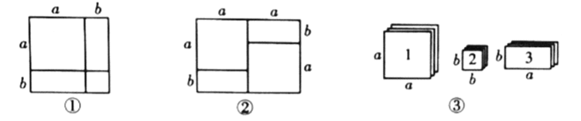
根据阅读材料回答下列问题:
(1)如图②所表示的因式分解的恒等式是________________________.
(2)现有足够多的正方形和长方形卡片(如图③),试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的长方形(每两张卡片之间既不重叠,也无空隙),使该长方形的面积为![]() ,并利用你画的长方形的面积对
,并利用你画的长方形的面积对![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于抛物线y=-x2+2x+3,有下列四个结论:①它的对称轴为x=1;
②它的顶点坐标为(1,4);
③它与y轴的交点坐标为(0,3),与x轴的交点坐标为(-1,0)和(3,0);
④当x>0时,y随x的增大而减小.
其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
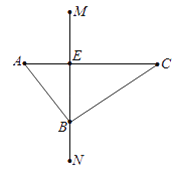
【题目】如图,南北向MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时50分,我国反走私A艇发现正东方有一走私艇以13海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇B密切注意.反走私艇A和走私艇C的距离是13海里,A、B两艇的距离是5海里;反走私艇B测得距离C艇12海里,若走私艇C的速度不变,最早会在什么时候进入我国领海?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个足球垂直水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤4).
(1)当t=3时,求足球距离地面的高度;
(2)当足球距离地面的高度为10米时,求t;
(3)若存在实数t1,t2(t1≠t2)当t=t1或t2时,足球距离地面的高度都为m(米),求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
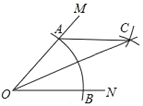
【题目】如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具厂生产一种课桌和椅子,课桌每张定价200 元,椅子每把定价80元,厂方在开展促销活动期间,向客户提供两种优惠方案:方案一:每买一张课桌就赠送一把椅子;方案二:课桌和椅子都按定价的80%付款.某校计划添置100张课桌和x把椅子.
(1)若x>100,请用含x的代数式分别把两种方案的费用表示出来;
(2)若x=300,如果两种方案可以同时使用,作为一种新的方案,请帮助学校设计一种最省钱的方案
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com