
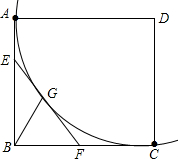
 如图,正方形ABCD的边长为6,以D为圆心、DA为半径作⊙D,E在AB上,AE=2,EF切⊙D于G,交BC于F,
如图,正方形ABCD的边长为6,以D为圆心、DA为半径作⊙D,E在AB上,AE=2,EF切⊙D于G,交BC于F,
| GH |
| BE |
| FG |
| EF |
| HF |
| BF |
| 4×3 |
| 5 |
| 12 |
| 5 |
| 9 |
| 5 |
| 6 |
| 5 |
| GH |
| BH |
| ||
|


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
 如图,有一块长为6.5单位长度,宽为2单位长度的长方形纸片,请把它分成6块,再拼成一个正方形,先在图中画出分割线,再画出拼后的图形,并标出相应的数据.
如图,有一块长为6.5单位长度,宽为2单位长度的长方形纸片,请把它分成6块,再拼成一个正方形,先在图中画出分割线,再画出拼后的图形,并标出相应的数据.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
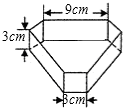 如图所示,是一种“口子窖”酒的包装纸盒,它的侧面由长方形和正方形组成.经测量,底面六变形有三条边的长是9cm,有三条边的长是3cm,每个内角都是120°,该六棱柱的高是3cm,请你设计一种裁剪方案,使之能制作这种无盖的包装盒.
如图所示,是一种“口子窖”酒的包装纸盒,它的侧面由长方形和正方形组成.经测量,底面六变形有三条边的长是9cm,有三条边的长是3cm,每个内角都是120°,该六棱柱的高是3cm,请你设计一种裁剪方案,使之能制作这种无盖的包装盒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com