
分析 (1)设A种奖品的单价是x元,B种奖品的单价是y元,根据“钱数=A种奖品单价×数量+B种奖品单价×数量”可列出关于x、y的二元一次方程组,解方程组即可得出结论;
(2)设购买A种奖品m件,则购买B种奖品(100-m)件,根据购买费用不超过1375元,且A种奖品的数量不大于B种奖品数量的4倍,可列出关于m的一元一次不等式组,解不等式组即可得出m的取值范围,再结合数量关系即可得出W与m之间的函数关系,根据一次函数的性质既可以解决最值问题.
解答 解:(1)设A种奖品的单价是x元,B种奖品的单价是y元,
由已知得:$\left\{\begin{array}{l}{3x+2y=80}\\{5x+4y=150}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=10}\\{y=25}\end{array}\right.$,
答:A种奖品的单价是10元,B种奖品的单价是25元.
(2)设购买A种奖品m件,则购买B种奖品(100-m)件,
由已知得:$\left\{\begin{array}{l}{10m+25×(100-m)≤1375}\\{m≤4×(100-m)}\end{array}\right.$,
解得:75≤m≤80.
∴W=10m+25×(100-m)=-15m+2500(75≤m≤80),
∵-15<0,
∴当m=80时,W取最小值,最小值为1300.
故W(元)与m(件)之间的函数关系式为W=-15m+2500(75≤m≤80),最少费用为1300元.
点评 本题考查了解二元一次方程组、一元一次不等式组以及一次函数的性质,解题的关键是:(1)列出关于x、y的二元一次方程组;(2)根据数量关系列出W关于m的函数关系式.本题属于中档题,难度不大,解决该题型题目时,根据数量关系列出方程(方程组、函数关系或不等式组)是关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | 3$\sqrt{2}-\sqrt{2}$=3 | C. | 2$\sqrt{3}×3\sqrt{3}=6\sqrt{3}$ | D. | ($\sqrt{8}-\sqrt{6}$)$÷\sqrt{2}=2-\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一批炮弹的杀伤力的情况 | B. | 了解一批灯泡的使用寿命 | ||
| C. | 全面人口普查 | D. | 全市学生每天参加体育锻炼的时间 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
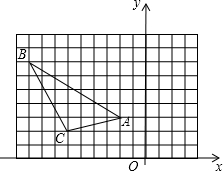 如图,在直角坐标系中,△ABC的顶点都在网格点上(方格纸中每个小正方形边长为1),将△ABC向右平移4格,再向下平移2格.
如图,在直角坐标系中,△ABC的顶点都在网格点上(方格纸中每个小正方形边长为1),将△ABC向右平移4格,再向下平移2格.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com