
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
【答案】
(1)
解:依题意得:  ,
,
解之得:  ,
,
∴抛物线解析式为y=﹣x2﹣2x+3
∵对称轴为x=﹣1,且抛物线经过A(1,0),
∴把B(﹣3,0)、C(0,3)分别代入直线y=mx+n,
得 ![]() ,
,
解之得: ![]() ,
,
∴直线y=mx+n的解析式为y=x+3
(2)
解:设直线BC与对称轴x=﹣1的交点为M,则此时MA+MC的值最小.
把x=﹣1代入直线y=x+3得,y=2,
∴M(﹣1,2),
即当点M到点A的距离与到点C的距离之和最小时M的坐标为(﹣1,2)
(3)
解:设P(﹣1,t),
又∵B(﹣3,0),C(0,3),
∴BC2=18,PB2=(﹣1+3)2+t2=4+t2,PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10,
①若点B为直角顶点,则BC2+PB2=PC2即:18+4+t2=t2﹣6t+10解之得:t=﹣2;
②若点C为直角顶点,则BC2+PC2=PB2即:18+t2﹣6t+10=4+t2解之得:t=4,
③若点P为直角顶点,则PB2+PC2=BC2即:4+t2+t2﹣6t+10=18解之得:t1= ![]() ,t2=
,t2= ![]() ;
;
综上所述P的坐标为(﹣1,﹣2)或(﹣1,4)或(﹣1, ![]() ) 或(﹣1,
) 或(﹣1, ![]() ).
).

【解析】(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;(2)设直线BC与对称轴x=﹣1的交点为M,则此时MA+MC的值最小.把x=﹣1代入直线y=x+3得y的值,即可求出点M坐标;(3)设P(﹣1,t),又因为B(﹣3,0),C(0,3),所以可得BC2=18,PB2=(﹣1+3)2+t2=4+t2 , PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.


科目:初中数学 来源: 题型:
【题目】已知:点A在射线CE上,∠C=∠D.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )

A. 88° B. 30° C. 32° D. 48°
查看答案和解析>>
科目:初中数学 来源: 题型:
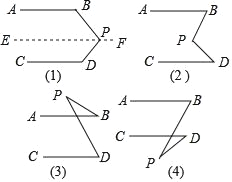
【题目】如图(1),AB∥CD,试求∠BPD与∠B、∠D的数量关系,说明理由.
(1)填空:
解:过点P作EF∥AB,
∴∠B+∠BPE=180°
∵AB∥CD,EF∥AB
∴ (如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∠EPD+ =180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(2)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的数量关系,并说明理由.
(3)观察图(3)和(4),已知AB∥CD,直接写出图中的∠BPD与∠B、∠D的数量关系,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°. 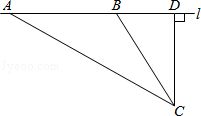
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.(参考数据: ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.

(1)请补全下表:
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
(2)填空:
由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,![]() ;当α=135°时,
;当α=135°时,![]() .由上表可以得到
.由上表可以得到![]() ( ______°);
( ______°);![]() ( ______°),…,由此可以归纳出
( ______°),…,由此可以归纳出![]() .
.
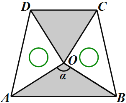
(3) 两块相同的等腰直角三角板按如图的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 2 | 5 | 1 | 5 | 4 | 7 | 4 | 3 | 3 | 6 |
根据以上数据,解答下列问题:
(I)直接填空:第10次摸棋子摸到黑棋子的频率为 ;
(Ⅱ)试估算袋中的白棋子数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连接DF,CF. 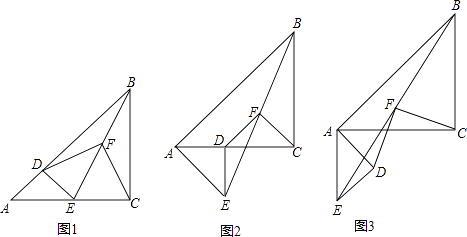
(1)如图1,当点D在AB上,点E在AC上,请直接写出此时线段DF,CF的数量关系和位置关系(不用证明); 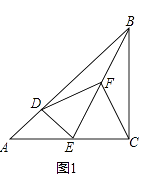
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断; 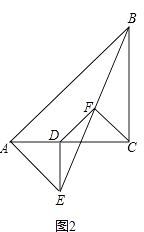
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC= ![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果). 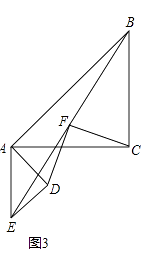
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com