
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (1)(4) | C. | (1)(2)(4) | D. | (2)(3)(4) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
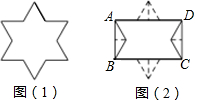 如图(1)是一个六角星的纸板,其中六个锐角都为60°,六个钝角都为120°,每条边都相等,现将该纸板按图(2)切割,并无缝隙无重叠地拼成矩形ABCD.若六角星纸板的面积为9$\sqrt{3}$cm2,则矩形ABCD的周长为( )
如图(1)是一个六角星的纸板,其中六个锐角都为60°,六个钝角都为120°,每条边都相等,现将该纸板按图(2)切割,并无缝隙无重叠地拼成矩形ABCD.若六角星纸板的面积为9$\sqrt{3}$cm2,则矩形ABCD的周长为( )| A. | 18cm | B. | 8$\sqrt{3}$cm | C. | (2$\sqrt{3}$+6)cm | D. | (6$\sqrt{3}$+6)cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴.y轴.只知道游乐园D的坐标为(2,-2),请你帮她画出坐标系,并写出其他各景点的坐标.
王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴.y轴.只知道游乐园D的坐标为(2,-2),请你帮她画出坐标系,并写出其他各景点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
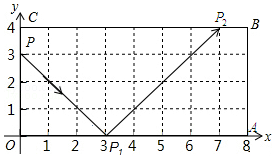 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P3的坐标是(8,3);点P2017的坐标是(3,0).
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时,记为点P1,第2次碰到矩形的边时,记为点P2,…第n次碰到矩形的边时,记为点Pn,则点P3的坐标是(8,3);点P2017的坐标是(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
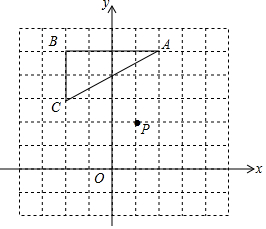 在如图所示的网格纸中,建立了平面直角坐标系xOy,点P(1,2),点A(2,5),B(-2,5),C(-2,3).
在如图所示的网格纸中,建立了平面直角坐标系xOy,点P(1,2),点A(2,5),B(-2,5),C(-2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com