
【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F. 
(1)求证:BD是⊙O的切线.
(2)若AB= ![]() ,E是半圆
,E是半圆 ![]() 上一动点,连接AE,AD,DE. 填空:
上一动点,连接AE,AD,DE. 填空:
①当 ![]() 的长度是时,四边形ABDE是菱形;
的长度是时,四边形ABDE是菱形;
②当 ![]() 的长度是时,△ADE是直角三角形.
的长度是时,△ADE是直角三角形.
【答案】
(1)证明:如图1,连接OD,

∵在Rt△ABC中,∠BAC=90°,∠C=30°,
∴AB= ![]() BC,
BC,
∵D是BC的中点,
∴BD= ![]() BC,
BC,
∴AB=BD,
∴∠BAD=∠BDA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODB=∠BAO=90°,
即OD⊥BC,
∴BD是⊙O的切线.
(2)![]() π;
π;![]() π或π
π或π
【解析】(2)①当DE⊥AC时,四边形ABDE是菱形; 如图2,设DE交AC于点M,连接OE,则DE=2DM,
∵∠C=30°,
∴CD=2DM,∴DE=CD=AB= ![]() BC,
BC,
∵∠BAC=90°,
∴DE∥AB,
∴四边形ABDE是平行四边形,
∵AB=BD,
∴四边形ABDE是菱形;
∵AD=BD=AB=CD= ![]() BC=
BC= ![]() ,
,
∴△ABD是等边三角形,OD=CDtan30°=1,
∴∠ADB=60°,
∵∠CDE=90°﹣∠C=60°,
∴∠ADE=180°﹣∠ADB﹣∠CDE=60°,
∴∠AOE=2∠ADE=120°,
∴ ![]() 的长度为:
的长度为: ![]() =
= ![]() π;
π;
故答案为: ![]() ;
;
②若∠ADE=90°,则点E与点F重合,此时 ![]() 的长度为:
的长度为: ![]() =π;
=π;
若∠DAE=90°,则DE是直径,则∠AOE=2∠ADO=60°,此时 ![]() 的长度为:
的长度为: ![]() =
= ![]() π;
π;
∵AD不是直径,
∴∠AED≠90°;
综上可得:当 ![]() 的长度是
的长度是 ![]() π或π时,△ADE是直角三角形.
π或π时,△ADE是直角三角形.
故答案为: ![]() π或π.
π或π.
(1)首先连接OD,由在Rt△ABC中,∠BAC=90°,∠C=30°,⊙O恰好经过边BC的中点D,易得AB=BD,继而证得∠ODB=∠BAC=90°,即可证得结论;(2)①易得当DE⊥AC时,四边形ABDE是菱形,然后求得∠AOE的度数,半径OD的长,则可求得答案;②分别从∠ADE=90°,∠DAE=90°,∠AED=90°去分析求解即可求得答案.


科目:初中数学 来源: 题型:
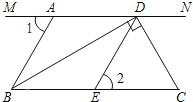
【题目】如图,MN∥BC,BD⊥DC,∠1=∠2=60°.
(1)AB 与 DE 平行吗?请说明理由;
(2)若 DC 是∠NDE 的平分线.
①试说明∠ABC=∠C;
②试说明 BD 是∠ABC 的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广电局与长江证券公司联合推出广电宽带网业务,用户通过宽带网可以享受新闻点播、影视欣赏、股市大户室等项服务,用户缴纳上网费的方式有:方式一:每月80元包月;方式二:每月上网费y(元)与上网时间x(小时)的函数关系用如图所示的折线表示;方式三:以0小时为起点,每小时收费1.6元,月收费不超过120元.若设一用户每月上网x小时,月上网费为y元.

(1)根据图象,写出方式二中y(元)与x(小时)的函数关系式;
(2)试写出方式三中y(元)与x(小时)的函数关系式;
(3)若此用户每月上网60小时,选用哪种方式上网其费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,P是菱形ABCD的对角线AC上一动点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,则△AMN的面积为y,则y关于x的函数图象的大致形状是( )
A.
B.
C.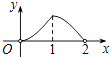
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个数的平方等于![]() ,记为
,记为![]() ,这个数
,这个数![]() 叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为![]() (
(![]() 、
、![]() 为实数),
为实数),![]() 叫这个复数的实部,
叫这个复数的实部, ![]() 叫做这个复数的虚部,它的加、减、乘法运算与整式的加、减、乘法运算类似.
叫做这个复数的虚部,它的加、减、乘法运算与整式的加、减、乘法运算类似.
例如计算: ![]() .
.
(![]() )填空:
)填空: ![]() __________,
__________, ![]() __________;
__________;
(![]() )计算:
)计算: ![]() ;
;
(![]() )试一试:请利用近期学习的有关知识和方法将
)试一试:请利用近期学习的有关知识和方法将![]() 化简成
化简成![]() 的形式.
的形式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今社会手机越来越普及,有很多人开始过份依赖手机,一天中使用手机时间过长而形成了“手机瘾”.为了解我校初三年级学生的手机使用情况,学生会随机调查了部分学生的手机使用时间,将调查结果分成五类:A、基本不用;B、平均一天使用1~2小时;C、平均一天使用2~4小时;D、平均一天使用4~6小时;E、平均一天使用超过6小时.并用得到的数据绘制成了如下两幅不完整的统计图(图1、2),请根据相关信息,解答下列问题: 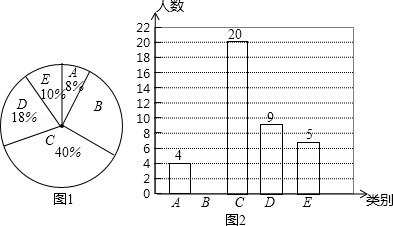
(1)将上面的条形统计图补充完整;
(2)若一天中手机使用时间超过6小时,则患有严重的“手机瘾”.我校初三年级共有1490人,试估计我校初三年级中约有多少人患有严重的“手机瘾”;
(3)在被调查的基本不用手机的4位同学中有2男2女,现要从中随机再抽两名同学去参加座谈,请你用列表法或树状图方法求出所选两位同学恰好是一名男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
请结合图表完成下列各题:
(1)①表中a的值为; ②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是 .
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com