
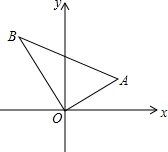
 如图,Rt△ABO的顶点在原点,OA=12,AB=20,∠AOx=30°,求A,B两点的坐标,并求△AOB的面积.
如图,Rt△ABO的顶点在原点,OA=12,AB=20,∠AOx=30°,求A,B两点的坐标,并求△AOB的面积. 分析 根据OA=12,∠AOx=30°,可以求得点A的坐标,根据OA和AB的长可以求得OB的长,从而可以求得点B的坐标,然后根据OA和OB的长可以求得△AOB的面积.
解答 解:∵OA=12,∠AOx=30°,
∴点A的横坐标是:OA•cos30°=12×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$,OA的纵坐标是:OA•sin30°=12×$\frac{1}{2}$=6,
即点A的坐标是(6$\sqrt{3}$,6),
∵∠AOB=90°,OA=12,AB=20,
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}=16$,
∴点B的横坐标是:-OB•cos60°=-$16×\frac{1}{2}$=-8,点B的纵坐标是:OB•sin60°=16×$\frac{\sqrt{3}}{2}$=8$\sqrt{3}$,
即点B的坐标是(-8,8$\sqrt{3}$),
∵OA=12,OB=16,∠AOB=90°,
∴△AOB的面积是$\frac{OA•OB}{2}=\frac{12×16}{2}=96$.
点评 本题考查坐标与图形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
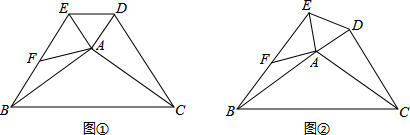
 如图,△ABC中,D是AB边上一点,⊙O过D,B,C三点,∠DOC=2∠ACD=90°.
如图,△ABC中,D是AB边上一点,⊙O过D,B,C三点,∠DOC=2∠ACD=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
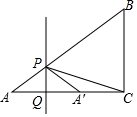 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,点P为线段AB上一动点,直线PQ⊥AC于点Q,点A关于PQ的对称点A′落在直线AC上,若△A′PC为等腰三角形,则AP的长为$\frac{20}{13}$.
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,点P为线段AB上一动点,直线PQ⊥AC于点Q,点A关于PQ的对称点A′落在直线AC上,若△A′PC为等腰三角形,则AP的长为$\frac{20}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x2-2x2+1 | B. | $\frac{5}{2}$xy4 | C. | $\frac{3bc}{a}$ | D. | $\frac{a}{2}$-b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
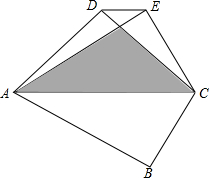 如图,由一副三角板组成的四边形ABCD中,∠B=∠ADC=90°,∠BAC=30°,把△ABC沿AC折叠,点B落在点E处,若两个三角形重叠部分的面积为2$\sqrt{3}$+2,则DE=$\sqrt{2}$.
如图,由一副三角板组成的四边形ABCD中,∠B=∠ADC=90°,∠BAC=30°,把△ABC沿AC折叠,点B落在点E处,若两个三角形重叠部分的面积为2$\sqrt{3}$+2,则DE=$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com