
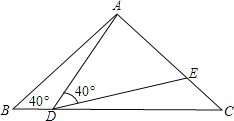
【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.

(1)当∠BDA=115°时,∠BAD= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
【答案】(1)25°;小.(2)当DC等于2时,△ABD≌△DCE;(3)当∠ADB=110°或80°时,△ADE是等腰三角形.
【解析】
试题分析:(1)根据三角形内角和定理,将已知数值代入即可求出∠BAD,根据点D的运动方向可判定∠BDA的变化情况.
(2)假设△ABD≌△DCE,利用全等三角形的对应边相等得出AB=DC=2,即可求得答案.
(3)假设△ADE是等腰三角形,分为三种情况:①当AD=AE时,∠ADE=∠AED=40°,根据∠AED>∠C,得出此时不符合;②当DA=DE时,求出∠DAE=∠DEA=70°,求出∠BAC,根据三角形的内角和定理求出∠BAD,根据三角形的内角和定理求出∠BDA即可;③当EA=ED时,求出∠DAC,求出∠BAD,根据三角形的内角和定理求出∠ADB.
解:(1)∠BAD=180°﹣∠ABD﹣∠BDA=180°﹣40°﹣115°=25°;
从图中可以得知,点D从B向C运动时,∠BDA逐渐变小;
故答案为:25°;小.
(2)当△ABD≌△DCE时.
DC=AB,
∵AB=2,
∴DC=2,
∴当DC等于2时,△ABD≌△DCE;
(3)∵AB=AC,
∴∠B=∠C=40°,
①当AD=AE时,∠ADE=∠AED=40°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=![]() (180°﹣40°)=70°,
(180°﹣40°)=70°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=100°﹣70°=30°;
∴∠BDA=180°﹣30°﹣40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°﹣40°=60°,
∴∠BDA=180°﹣60°﹣40°=80°;
∴当∠ADB=110°或80°时,△ADE是等腰三角形.


科目:初中数学 来源: 题型:
【题目】长沙市马王堆蔬菜批发市场某批发商原计划以每千克10元的单价对外批发销售某种蔬菜![]() 为了加快销售,该批发商对价格进行两次下调后,售价降为每千克
为了加快销售,该批发商对价格进行两次下调后,售价降为每千克![]() 元.
元.
![]() 求平均每次下调的百分率;
求平均每次下调的百分率;
![]() 某大型超市准备到该批发商处购买2吨该蔬菜,因数量较多,该批发商决定再给予两种优惠方案以供选择
某大型超市准备到该批发商处购买2吨该蔬菜,因数量较多,该批发商决定再给予两种优惠方案以供选择![]() 方案一:打八折销售;方案二:不打折,每吨优惠现金1000元
方案一:打八折销售;方案二:不打折,每吨优惠现金1000元![]() 试问超市采购员选择哪种方案更优惠?请说明理由.
试问超市采购员选择哪种方案更优惠?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC和△DCE均是等边三角形,点B. C. E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论中:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC,正确的是( )个

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,D是AC的中点,E是AB的中点,作EF⊥BC于F,延长BC至G,使CG=BF,连接CE、DE、DG.

(1)如图1,求证:四边形CEDG是平行四边形;
(2)如图2,连接EG交AC于点H,若EG⊥AB,请直接写出图2中所有长度等于![]() GH的线段.
GH的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”,
(1)如图△ABC中,AB=AC=![]() ,BC=2,求证:△ABC是“美丽三角形”;
,BC=2,求证:△ABC是“美丽三角形”;
(2)在Rt△ABC中,∠C=90°,AC=2![]() ,若△ABC是“美丽三角形”,求BC的长.
,若△ABC是“美丽三角形”,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.

(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,将△ACE沿着AE折叠以后C点正好落在AB边上的点D处.
(1)当∠B=28°时,求∠AEC的度数;
(2)当AC=6,AB=10时,
①求线段BC的长;
②求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AD∥BC,M为CD中点,AM平分∠DAB,AD+BC=AB.求证:BM平分∠ABC.

小淇证明过程如下:
延长BC至点F,使得CF=AD,连接MF.
∵ AD∥BC, ∴ ∠D=∠MCF.
∵ M为CD中点,∴ DM=CM.
在△ADM和△FCM中,

∴ △ADM≌△FCM(SAS). ∴ AM=FM.
∵ BF=BC+CF=BC+AD=AB,∴ △ABF是等腰三角形.
∴ BM平分∠ABC(等腰三角形底边上的中线与顶角的角平分重合).
(1)请你简要叙述小淇证明方法的错误之处;
(2)若AB=5,AM=3,求四边形ABCD面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年7月1日起,重庆实施阶梯电价,市民家庭每月用电量使用情况不同,按照用电量区间价格缴纳用电费用.其收费标准如下表:阶梯电价分三个档次.设某用户每月用电量为x度,应交电费为y元.
档次 | 用电量 | 每度电价格 |
第一档 | 不超过200度的部分 | 0.52元 |
第二档 | 超过200度不超过400度的部分 | 0.57元 |
第三档 | 超过400度的部分 | 0.82元 |
(1)直接写出y与x的关系式;
(2)小明家6、7月份共用电800度,应交电费471元,已知7月份的用电量比6月份的用电量大,求小明家6、7月份各用电多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com