解:(1)∵|a+2|+|b-6|=0,
∴a+2=0,b-6=0,
解得,a=-2,b=6,
∴点A表示的数为-2,点B表示的数为 6.
故填:-2、6;
(2)设数轴上点C表示的数为c.
∵AC=2BC,
∴|c-a|=2|c-b|,即|c+2|=2|c-6|.
∵AC=2BC>BC,
∴点C不可能在BA的延长线上,则C点可能在线段AB上和线段AB的延长线上.
①当C点在线段AB上时,则有-2≤c≤6,
得c+2=2(6-c),解得c=

;
②当C点在线段AB的延长线上时,则有c>6,
得c+2=2(c-6),解得c=14.
故当AC=2BC时,c=

或c=14;
故填:14或

;
(3)①∵甲球运动的路程为:1•t=t,OA=2,
∴甲球与原点的距离为:t+2;
乙球到原点的距离分两种情况:
(Ⅰ)当0<t≤3时,乙球从点B处开始向左运动,一直到原点O,
∵OB=6,乙球运动的路程为:2•t=2t,
乙到原点的距离:6-2t(0≤t≤3)
(Ⅱ)当t>3时,乙球从原点O处开始一直向右运动,
此时乙球到原点的距离为:2t-6 (t>3);
②当0<t≤3时,得t+2=6-2t,
解得t=

;
当t>3时,得t+2=2t-6,
解得t=8.
故当t=

秒或t=8秒时,甲乙两小球到原点的距离相等.
分析:(1)根据非负数的性质求得a=-2,b=6;
(2)分C点在线段AB上和线段AB的延长线上两种情况讨论即可求解;
(3)①甲球到原点的距离=甲球运动的路程+OA的长,乙球到原点的距离分两种情况:(Ⅰ)当0<t≤3时,乙球从点B处开始向左运动,一直到原点O,此时OB的长度-乙球运动的路程即为乙球到原点的距离;(Ⅱ)当t>3时,乙球从原点O处开始向右运动,此时乙球运动的路程-OB的长度即为乙球到原点的距离;
②分两种情况:(Ⅰ)0<t≤3,(Ⅱ)t>3,根据甲、乙两小球到原点的距离相等列出关于t的方程,解方程即可.
点评:本题考查了非负数的性质,方程的解法,数轴,两点间的距离,有一定难度,运用分类讨论思想、方程思想及数形结合思想是解题的关键.

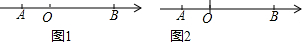
 ;
; 或c=14;
或c=14; ;
; ;
; 秒或t=8秒时,甲乙两小球到原点的距离相等.
秒或t=8秒时,甲乙两小球到原点的距离相等.


 数学魔术:如图所示,数轴上的点A、B、C、D分别表示-3,-1
数学魔术:如图所示,数轴上的点A、B、C、D分别表示-3,-1 探索性问题:
探索性问题: