
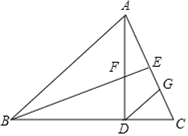
【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点且BE平分∠ABD,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
求证:
(1)∠BAD=2∠DAC
(2)EF=EG.
【答案】见解析
【解析】试题分析:
(1)由AB=AC,E是AC的中点,可得BE⊥AC,∠DBA=2∠DBF;结合AD⊥BC可证得∠DBF=∠DAC,从而可证△BDF≌△ADC,得到AD=BD,
∴∠DAB=∠DBA=2∠DBF=2∠DAC;
(2)如图,延长BE、DG交于点K,①由DG∥AB和BE平分∠ABC可得∠K=∠DAK=∠DAC,从而可得DK=DB=DA;②由AB=BC,DG∥AB可得∠DGC=∠C,从而可得DG=DC=DF,由①②可得AD-DF=DK-DG,即AF=KG,最后通过证△AEF≌△KEG可得EF=EG.

试题解析:
(1)∵AD⊥BC,∴∠ADC=∠BDF=90°,
∵AB=BC,E为AC的中点,
∴∠DBA=2∠CBE,BE⊥AC,
∴∠BEC=90°,
∴180°-∠C-∠ADC=180°-∠C-∠BEC,
即∠DBF=∠CAD,
在△BDF和△ADC中,
∠BDF=∠ADC=90°,∠DBF=∠CAD,BF=AC,
∴△BDF≌△ADC,
∴BD=AD,
∴∠BAD=∠ABD=2∠CBE=2∠DAC。
(2)延长BE、DG交于点k,

∵DG//AB,
∴∠CGD=∠CAB,∠k=∠ABE,
∵∠BAC=∠C,
∴∠CGD =∠C,
∵∠K=∠CBE=∠CAD,
∠AEF=∠KEG=90°,∠EAF=∠EKG,
∴DG=DC,DK=BD,
∴DG=DF,DK=BD=AD,
∴DK-DG=AD-DF,即GK=AF,
在Rt△AEF和Rt△KEG中,
∠AEF=∠KEG=90°,∠EAF=∠K,AF=GK,
∴Rt△AEF≌ Rt△KEG,
∴EF=EG.


科目:初中数学 来源: 题型:
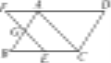
【题目】如图,在□ABCD中,点E在边BC上,点F在边DA的延长线上,且AF=CE,EF与AB交于点G.
(1)求证:AC∥EF;
(2)若点G是AB的中点,BE=6,求边AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若我们规定三角“![]() ”表示为:abc;方框“
”表示为:abc;方框“![]() ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如:![]() =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
(1)计算:![]() = ______ ;
= ______ ;
(2)代数式 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;
(3)解方程:![]() =6x2+7.
=6x2+7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面镜反射光线的规律:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图①,一束光线m射到平面镜a上,被a反射后的光线为n,则入射光线m、反射光线n与平面镜a所夹的锐角相等,即∠1=∠2.
如图②所示,AB,CD为两面平面镜,经过两次反射后,入射光线m与反射光线n之间的位置关系会随之改变,请你计算:图②中,当两平面镜AB,CD的夹角∠ABC是多少度时,可以使入射光线m与反射光线n平行但方向相反.
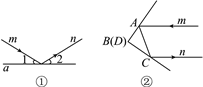
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2 , 其中正确结论是(填序号)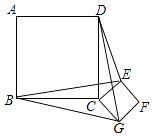
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出A′、B′、C′的坐标,并在图中画出平移后图形;
(3)求出△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com