
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),蓝球1个.若从中任意摸出一个球,它是蓝球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)从袋中一次摸出两个球,请用画树状图或列表格的方法列出所有等可能的结果,并求出摸到两个不同颜色球的概率.
科目:初中数学 来源: 题型:
【题目】田忌赛马的故事为我们所熟知.小亮与小齐学习概率初步知识后设计了如下游戏:小亮手中有方块l0、8、6三张扑克牌,小齐手中有方块9、7、5三张扑克牌.每人从各自手中取一张牌进行比较,数字大的为本“局”获胜,每次取的牌不能放回.
(1)若每人随机取手中的一张牌进行比赛,求小齐本“局”获胜的概率;
(2)若比赛采用三局两胜制,即胜2局或3局者为本次比赛获胜者.当小亮的三张牌出牌顺序为先出6,再出8,最后出l0时,小齐随机出牌应对,求小齐本次比赛获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,点E、F分别为正方形ABCD的边BC、CD上一点,AC、BD交于点O,且∠EAF=45°,AE,AF分别交对角线BD于点M,N,则有以下结论:①△AOM∽△ADF;②EF=BE+DF;③∠AEB=∠AEF=∠ANM;④S△AEF=2S△AMN,以上结论中,正确的个数有( )个.
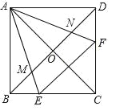
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°.现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )
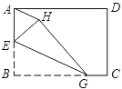
A. 5B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
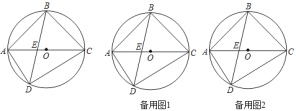
【题目】如图,四边形ABCD内接于⊙O.AC为直径,AC、BD交于E,![]() =
=![]() .
.
(1)求证:AD+CD=![]() BD;
BD;
(2)过B作AD的平行线,交AC于F,求证:EA2+CF2=EF2;
(3)在(2)条件下过E,F分别作AB、BC的垂线垂足分别为G、H,连GH、BO交于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,2),
(1)求抛物线的函数表达式;
(2)如图,在抛物线对称轴上取两个点G、H(G在H的上方),且满足GH=1,连接CG,AH,求四边形CGHA的周长的最小值;
(3)如图,点P是抛物线第一象限的一个动点,过点P作PQ⊥x轴于点Q,交BC于点D,PE⊥BC于点E,设△PDE的面积为S,求当S取得最大值时点P的坐标,并求S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与直线
与直线![]() 分别交于
分别交于![]() 轴、
轴、![]() 轴上的
轴上的![]() 两点,设该抛物线与
两点,设该抛物线与![]() 轴的另一个交点为点
轴的另一个交点为点![]() ,顶点为点
,顶点为点![]() ,联结
,联结![]() 交
交![]() 轴于点
轴于点![]() .
.

![]() 求该抛物线的表达式及点
求该抛物线的表达式及点![]() 的坐标;
的坐标;
![]() 求
求![]() 的正切值;
的正切值;
![]() 如果点
如果点![]() 在
在![]() 轴上,且
轴上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个函数![]() 和
和![]() ,若对于每个使函数有意义的实数
,若对于每个使函数有意义的实数![]() ,函数
,函数![]() 的值为两个函数值中中较小的数,则称函数
的值为两个函数值中中较小的数,则称函数![]() 为这两个函数
为这两个函数![]() 、
、![]() 的较小值函数。例如:
的较小值函数。例如:![]() ,
,![]() ,则
,则![]() 、
、![]() 的较小值函数
的较小值函数![]()
(1)函数![]() 是函数
是函数![]() ,
,![]() 的较小值函数;
的较小值函数;
①在如图的平面直角坐标系中画出函数![]() 的图像.
的图像.
②写出函数![]() 的两条性质.
的两条性质.
(2)函数![]() 是函数
是函数![]() ,
,![]() 的较小值函数,当
的较小值函数,当![]() 时,函数值
时,函数值![]() 的取值范围为
的取值范围为![]() .当
.当![]() 取某个范围内的任意值时,
取某个范围内的任意值时,![]() 为定值.直接写出满足条件的
为定值.直接写出满足条件的![]() 的取值范围及其对应的
的取值范围及其对应的![]() 值.
值.
(3)函数![]() 是函数
是函数![]() ,
,![]() (
(![]() 为常数,且
为常数,且![]() )的较小值函数,当
)的较小值函数,当![]() 时,随着
时,随着![]() 的增大,函数值
的增大,函数值![]() 先增大后减小,直接写出
先增大后减小,直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )

A. 6→3 B. 7→16 C. 7→8 D. 6→15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com