Question

5．已知山脚与山顶之间的距离为600米，甲上山过程中距离山脚的路程S（米）与行走时间t（分）之间的函数图象如图1，乙上山、下山过程中距离山脚的路程S（米）与行走时间t（分）之间的函数图象如图2所示．

（1）两人同时出发前往山顶，乙到达山顶后立即返回，出发多长时间后两人相遇？
（2）如果甲晚出发5分钟，甲、乙两人在行走过程中何时相距15米？

Answer 1

分析 （1）待定系数法先求出甲出发前往山顶时、乙从山顶返回山脚时S关于t的函数解析式，根据题意列方程求解可得；
（2）分三种情况：①乙出发而甲还未出发，②乙下山还未与甲相遇，③乙下山与甲相遇后，分别列方程求解可得．

解答 解：（1）设甲出发前往山顶时，S关于t的函数解析式为：S=kt，
将（40，600）代入，得：600=40k，
解得：k=15，
∴S=15t；
设乙从山顶返回山脚的距离S关于时间t的函数解析式为：S=mx+n，
将（30，600）、（45，0）代入，得：$\left\{\begin{array}{l}{30m+n=600}\\{45m+n=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{m=-40}\\{n=1800}\end{array}\right.$，
∴S=-40t+1800，
根据题意得：$\left\{\begin{array}{l}{S=15t}\\{S=-40t+1800}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{t=\frac{360}{11}}\\{S=\frac{5400}{11}}\end{array}\right.$，
答：出发$\frac{360}{11}$分钟后两人相遇；

（2）如图：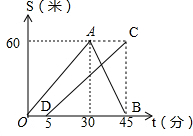

分以下3种情况：
①∵l_OA：y=20x，20x=15，
∴x=$\frac{3}{4}$；
②∵l_CD：y=15x-75，
∴-40x+1800-（15x-75）=15，
解得：x=$\frac{372}{11}$；
③（15x-75）-（-40x+1800）=15，
∴x=$\frac{378}{11}$；
答：甲、乙两人在t=$\frac{3}{4}$、$\frac{372}{11}$、$\frac{378}{11}$时相距15千米．

点评 本题主要考查一次函数的应用，待定系数求函数解析式是解题的根本，全面考虑两人相距15千米的情况是解题的关键．