
 如图,在△ABC中,AB=AC=4,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=4,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.分析 (1)根据AB=AC可得出∠C=40°,再根据平角为180°以及三角形内角和为180°即可算出∠EDC以及∠DEC的度数;
(2)根据三角形的内角和为180°即可得出∠BDA=140°-∠BAD,再根据∠BAD逐渐变大即可得出∠BDA逐渐变小;
(3)根据平角为180°以及三角形内角和为180°通过角的计算即可得出∠EDC=∠DAB,结合∠B=∠C即可得出△ABD∽△DCE,再根据△ABD≌△DCE利用全等三角形的性质即可得出DC=AB=4;
(4)分AD=AE、DA=DE以及EA=ED三种情况考虑△ADE为等腰三角形,根据等腰三角形的性质结合角的计算求出∠BDA的度数即可得出结论.
解答 解:(1)∵AB=AC=4,∠B=40°,
∴∠C=40°.
∵∠BDA+∠ADE+∠EDC=180°,∠ADE=40°,∠BDA=115°,
∴∠EDC=180°-115°-40°=25°.
∵∠EDC+∠C+∠DEC=180°,
∴∠DEC=180°-25°-40°=115°.
故答案为:25;115.
(2)∵∠B+∠BDA+∠BAD=180°,
∴∠BDA=180°-∠B-∠BAD=140°-∠BAD.
∵随着点D从B向C运动,∠BAD越来越大,
∴点D从B向C运动时,∠BDA逐渐变小.
故答案为:小.
(3)当DC=4时,△ABD≌△DCE,理由如下:
∵∠EDC+∠EDA+∠ADB=180°,∠DAB+∠B+∠ADB=180°,∠B=∠EDA=40°,
∴∠EDC=∠DAB.
∵∠B=∠C,
∴△ABD∽△DCE.
∴当DC=AB=4时,△ABD≌△DCE.
(4)△ADE为等腰三角形分三种情况:
①AD=AE.
∵∠ADE=40°,AD=AE,
∴∠AED=∠ADE=40°,∠DAE=180°-∠ADE-∠AED=100°.
∵∠BAC=180°-∠B-∠C=100°,D不与B、C重合,
∴∠DAE<∠BAC,即100°<100°,
∴AD≠AE;
②DA=DE.
∵∠ADE=40°,DA=DE,
∴∠DAE=∠DEA=$\frac{1}{2}$(180°-∠ADE)=70°,
∴∠BDA=∠DEC=180°-∠AED=110°;
③EA=ED.
∵∠ADE=40°,EA=ED,
∴∠EAD=∠EDA=40°,∠AED=180°-∠EAD-∠EDA=100°,
∴∠BDA=∠DEC=180°-∠AED=80°.
综上可知:在点D的运动过程中,△ADE的形状可以是等腰三角形,此时∠BDA的度数为80°或110°.
点评 本题考查了等腰三角形的性质、三角形内角和定理、相似三角形的判定以及全等三角形的性质,解题的关键是:(1)通过角的计算求出∠EDC以及∠DEC的度数;(2)找出∠BDA=140°-∠BAD;(3)根据全等三角形的性质找出DC=AB;(4)分AD=AE、DA=DE以及EA=ED三种情况考虑.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:填空题
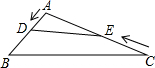 如图,在钝角△ABC中,AB=3cm,AC=6cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为3cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是$\frac{6}{5}$秒或$\frac{12}{7}$秒.
如图,在钝角△ABC中,AB=3cm,AC=6cm,动点D从点A出发到点B止.动点E从点C出发到点A止.点D运动的速度为1cm/s,点E运动的速度为3cm/s.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时.运动的时间是$\frac{6}{5}$秒或$\frac{12}{7}$秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com