
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与x轴负半轴交于B,与正半轴交于点
,与x轴负半轴交于B,与正半轴交于点![]() ,且
,且![]() .
.
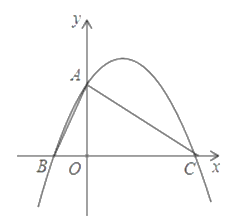
(1)求该二次函数解析式;
(2)若![]() 是线段
是线段![]() 上一动点,作
上一动点,作![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() 当
当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)若点![]() 为
为![]() 轴上方的抛物线上的一个动点,连接
轴上方的抛物线上的一个动点,连接![]() ,设所得
,设所得![]() 的面积为
的面积为![]() .问:是否存在一个
.问:是否存在一个![]() 的值,使得相应的点
的值,使得相应的点![]() 有且只有
有且只有![]() 个,若有,求出这个
个,若有,求出这个![]() 的值,并求此时点
的值,并求此时点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在一个
;(3)存在一个![]() 的值,使得相应的点
的值,使得相应的点![]() 有且只有
有且只有![]() 个,这个
个,这个![]() 的值为16,此时点
的值为16,此时点![]() 的横坐标为4或
的横坐标为4或![]() .
.
【解析】
(1)先根据点A、C的坐标得出OA、OC的长,再根据相似三角形的判定与性质求出OB的长,从而可得点B的坐标,然后根据点B、C的坐标可设二次函数解析式的交点式,最后将点A的坐标代入求解即可得;
(2)先根据点B、C的坐标求出BC的长,从而可得![]() 面积,设
面积,设![]() ,则
,则![]() ,再根据相似三角形的判定与性质可得
,再根据相似三角形的判定与性质可得![]() 面积,然后利用
面积,然后利用![]() 面积减去
面积减去![]() 面积可得
面积可得![]() 面积,最后利用二次函数的性质即可得;
面积,最后利用二次函数的性质即可得;
(3)先利用待定系数法求出直线AC的解析式,设![]() ,从而可得
,从而可得![]() ,再分
,再分![]() 和
和![]() 两种情况,分别求出S与m之间的函数表达式,然后利用二次函数的性质求出S的取值范围,找出符合条件的S值即可.
两种情况,分别求出S与m之间的函数表达式,然后利用二次函数的性质求出S的取值范围,找出符合条件的S值即可.
(1)![]()
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
![]() ,即
,即![]()
解得![]()
![]() 点B的坐标为
点B的坐标为![]()
由![]() 可设二次函数的解析式为
可设二次函数的解析式为![]()
将![]() 代入得:
代入得:![]()
解得![]()
则二次函数的解析式为![]()
故二次函数的解析式为![]() ;
;
(2)![]()
![]()
![]()
设![]() ,则
,则![]()
![]()
![]()
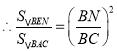 ,即
,即![]()
![]()
![]()
![]()
![]()
由二次函数的性质可知,当![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]()
故当![]() 面积最大时,点
面积最大时,点![]() 的坐标为
的坐标为![]() ;
;

(3)设直线AC的解析式为![]()
将![]() 得
得![]() ,解得
,解得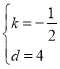
直线AC的解析式为![]()
设![]()
因为点![]() 为
为![]() 轴上方的抛物线上的一个动点
轴上方的抛物线上的一个动点
所以![]()
由题意,分以下两种情况:
①当![]() 时
时
如图1,过![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于
于![]() ,则
,则![]()
![]()
则![]()
![]()
![]()
![]()
由二次函数的性质可知,当![]() 时,S随m的增大而增大;当
时,S随m的增大而增大;当![]() 时,S随m的增大而减小
时,S随m的增大而减小
则此时S的最大值为![]() ,最小值为
,最小值为![]()
即有![]()
②当![]() 时
时
如图2,过![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 延长线于
延长线于![]() ,则
,则![]()
![]()
则![]()
![]()
![]()
![]()
![]()
由二次函数的性质可知,当![]() 时,S随m的增大而减小
时,S随m的增大而减小
则此时S的最大值为![]() ,最小值为
,最小值为![]()
即有![]()
由二次函数的图象与性质可得如下结论:
当![]() 时,在
时,在![]() 范围内没有相应的点
范围内没有相应的点![]() ,在
,在![]() 范围内相应的点
范围内相应的点![]() 有1个,即共有1个
有1个,即共有1个
当![]() 时,在
时,在![]() 范围内相应的点
范围内相应的点![]() 有2个,在
有2个,在![]() 范围内相应的点
范围内相应的点![]() 有1个,即共有3个
有1个,即共有3个
当![]() 时,在
时,在![]() 范围内相应的点
范围内相应的点![]() 有1个,在
有1个,在![]() 范围内相应的点
范围内相应的点![]() 有1个,即共有2个
有1个,即共有2个
当![]() 时,在
时,在![]() 范围内没有相应的点
范围内没有相应的点![]() ,在
,在![]() 范围内相应的点
范围内相应的点![]() 有1个,即共有1个
有1个,即共有1个
由此可知,当![]() 时,相应的点
时,相应的点![]() 有且只有
有且只有![]() 个
个
在![]() 范围内,当
范围内,当![]() 时,
时,![]()
在![]() 范围内,当
范围内,当![]() 时,
时,![]() ,解得
,解得![]() 或
或![]() (不符题设,舍去)
(不符题设,舍去)
综上,存在一个![]() 的值,使得相应的点
的值,使得相应的点![]() 有且只有
有且只有![]() 个,这个
个,这个![]() 的值为16,此时点
的值为16,此时点![]() 的横坐标为4或
的横坐标为4或![]() .
.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
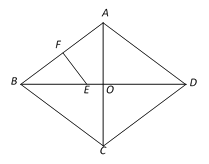
【题目】如图,点O是菱形ABCD对角线的交点,点E在BO上,EF垂直平分AB,垂足为F.
(1)求证:△BEF ∽△DCO;
(2)若AB=10,AC=12,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
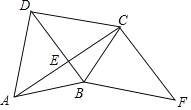
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠F=45°,BD=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
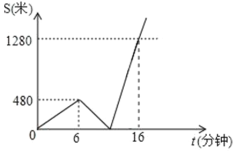
【题目】小明步行从家去火车站,走到6分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,那么从家到火车站路程是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线与![]() 轴交于点A,与
轴交于点A,与![]() 轴交点C,抛物线
轴交点C,抛物线![]() 过A,C两点,与x轴交于另一点B.
过A,C两点,与x轴交于另一点B.
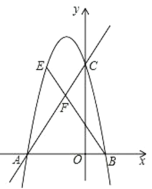
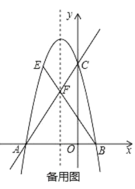
(1)求抛物线的解析式.
(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当![]() 时,求sin∠EBA的值.
时,求sin∠EBA的值.
(3)点N是抛物线对称轴上一点,在(2)的条件下,若点E位于对称轴左侧,在抛物线上是否存在一点M,使以M,N,E,B为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,对称轴是直线
,对称轴是直线![]() ,与
,与![]() 轴交于点
轴交于点![]() .若点
.若点![]() ,
,![]() 同时从
同时从![]() 点出发,都以每秒
点出发,都以每秒![]() 个单位长度的速度分别沿
个单位长度的速度分别沿![]() ,
,![]() 边运动.
边运动.
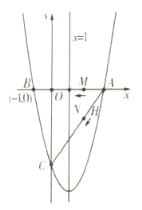
(1)求该二次函数的解析式及点![]() 的坐标,与
的坐标,与![]() 轴的另一个交点
轴的另一个交点![]() 的坐标.
的坐标.
(2)当![]() ,
,![]() 运动到
运动到![]() 秒时,
秒时,![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 轴上
轴上![]() 点处,请判定此时四边形
点处,请判定此时四边形![]() 的形状,并求出
的形状,并求出![]() 点坐标.
点坐标.
(3)当点![]() 运动到对称轴与
运动到对称轴与![]() 的交点时,点
的交点时,点![]() 往回运动,同时点
往回运动,同时点![]() 则
则![]() 倍的速度继续沿
倍的速度继续沿![]() 运动,在整个运动过程中,以点
运动,在整个运动过程中,以点![]() ,
,![]() ,
,![]() 为顶点的三角形面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
为顶点的三角形面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
(4)在![]() 段的抛物线上有一点
段的抛物线上有一点![]() 到线段
到线段![]() 的距离最大,请求出这个最大距离.
的距离最大,请求出这个最大距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生新冠疫情防控期间每天居家体育活动的时间(单位:![]() ),在网上随机调查了该校九年级部分学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
),在网上随机调查了该校九年级部分学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
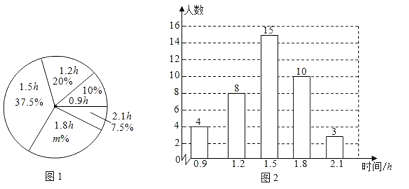
(1)本次接受调查的初中学生人数为________,图①中![]() 的值为________;
的值为________;
(2)这组数据的平均数是________,众数是________,中位数是________;
(3)根据统计的这组每天居家体育活动时间的样本数据,估计该校500名九年级学生居家期间每天体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com