
��֪����ͼ������������y��ax��ͼ���뷴��������y��![]() ��ͼ���ڵ�A(3��2)��
��ͼ���ڵ�A(3��2)��
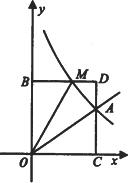
(1)ȷ�����������������ͷ����������ı���ʽ
(2)����ͼ��ش��ڵ�һ�����ڣ���xȡ��ֵʱ��������������ֵ����������������ֵ��
(3)M(m��n)�Ƿ���������ͼ���ϵ�һ�����㣬����0��m��3������M��ֱ��MB��x�ᣬ��y���ڵ�B������A��ֱ��AC��y�ύx���ڵ�C����ֱ��MB�ڵ�D�����ı���OADM�����Ϊ6ʱ�����ж��߶�BM��DM�Ĵ�С��ϵ����˵�����ɣ�
 ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д� Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
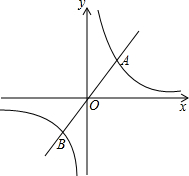 ��ͼ����֪����������y=x�뷴��������y=
��ͼ����֪����������y=x�뷴��������y=| 1 | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| x |
| 1 |
| x |
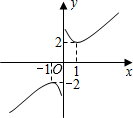 ����˫�������dz�֮Ϊ��˫�������������������м������⣺
����˫�������dz�֮Ϊ��˫�������������������м������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
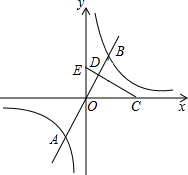 ��ͼ����֪����������y=ax��a��0����ͼ���뷴��������y=
��ͼ����֪����������y=ax��a��0����ͼ���뷴��������y=| k | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��֪����������y1=x������������y2=
��֪����������y1=x������������y2=| 1 |
| x |
| 1 |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ΪM��������������y=kx��ͼ������κ����ཻ������D��E����P���߶�DE���е㣮
ΪM��������������y=kx��ͼ������κ����ཻ������D��E����P���߶�DE���е㣮| 93 |
| 16 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com