
【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3 ![]() ,BG=4,则GH的长为 .
,BG=4,则GH的长为 . 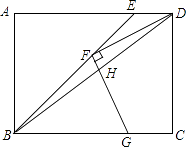
【答案】![]()
【解析】解:解法一:如右图,过点F作BC的垂线,分别交BC、AD于点M、N,则MN⊥AD,延长GF交AD于点Q,如图所示.
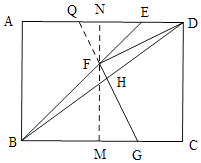
∵四边形ABCD是矩形,
∴∠ABC=90°,AD∥BC,
∵BE平分∠ABC,
∴∠ABE=∠EBC=45°,
∴△MBF是等腰直角三角形,
∵BF=3 ![]() ,
,
∴BM=FM=3,
∵BG=4,
∴MG=1,
∵FD⊥FG,
∴∠DFG=90°,
∴∠DFN+∠MFG=90°,
∵∠DNF=90°,
∴∠NDF+∠DFN=90°,
∴∠NDF=∠MFG,
在DNF和△FMG中,
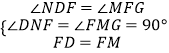 ,
,
∴△DNF≌△FMG(AAS),
∴DN=FM=3,NF=MG=1,
由勾股定理得:FG=FD= ![]() ,
,
∵QN∥BC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴FQ= ![]() ,QN=
,QN= ![]() ,
,
设GH=x,则FH= ![]() ﹣x,
﹣x,
∵QD∥BG,
∴ ![]() ,
,
∴ ![]() ,
,
x= ![]() ,
,
即GH= ![]() .
.
解法二:如右图,过F作FN⊥BC于N,过B作BM⊥FG于M,
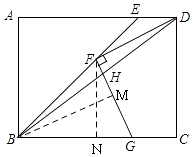
∵四边形ABCD是矩形,
∴∠ABC=90°,AD∥BC,
∵BE平分∠ABC,
∴∠ABE=∠EBC=45°,
∴△NBF是等腰直角三角形,
∵BF=3 ![]() ,
,
∴BN=FN=3,
∵BG=4,
∴NG=1,
在Rt△FNG中,由勾股定理得:DF=FG= ![]() =
= ![]() ,
,
∵S△BFG= ![]() BGFN=
BGFN= ![]() FGBM,
FGBM,
∴4×3= ![]() BM,
BM,
∴BM= ![]() ,
,
∴GM= ![]() =
= ![]() =
= ![]() ,
,
∴FM=GF﹣GM= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∵DF∥BM,
∴△DFH∽△BMH,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴HM= ![]() ,
,
∴GH=HM+GM= ![]() +
+ ![]() =
= ![]() ;
;
所以答案是: ![]() .
.
【考点精析】本题主要考查了三角形的面积和矩形的性质的相关知识点,需要掌握三角形的面积=1/2×底×高;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】(1)在如图所示的平面直角坐标系中,依次连接下列各点: A(-5,0),B(1,4),C(3,3),D(1,0),E(3,-3),F(1,-4).

(2)请你在如图所示的方格纸上按照如下要求设计直角三角形:

①使它的三边中有一边边长不是有理数;
②使它的三边中有两边边长不是有理数;
③使它的三边边长都不是有理数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.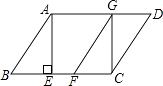
(1)求证:BE=DG;
(2)已知tanB= ![]() ,AB=5,若四边形ABFG是菱形,求平行四边形ABCD的面积.
,AB=5,若四边形ABFG是菱形,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4),
(1)画出△ABC关于y轴的对称图形△A1B1C1,并写出点B1的坐标;
(2)在x轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标.
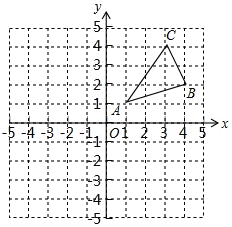
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 . 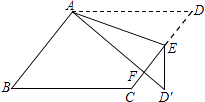
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
(1)求A、B两种品牌服装每套进价分别为多少元?
(2)该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
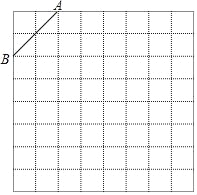
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ;
(3)求△ABC中BC边上的高长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com