
”¾ĢāÄæ”æŅŃÖŖ£¬ČēĶ¼A”¢B·Ö±šĪŖŹżÖįÉĻµÄĮ½µć£¬Aµć¶ŌÓ¦µÄŹżĪŖ-10£¬Bµć¶ŌÓ¦µÄŹżĪŖ90£®
![]()
£Ø1£©ĒėŠ“³öÓėA£¬BĮ½µć¾ąĄėĻąµČµÄMµć¶ŌÓ¦µÄŹż£»””
£Ø2£©ĻÖŌŚÓŠŅ»Ö»µē×ÓĀģŅĻP“ÓBµć³ö·¢Ź±£¬ŅŌ3øöµ„Ī»/ĆėµÄĖŁ¶ČĻņ×óŌĖ¶Æ£¬Ķ¬Ź±ĮķŅ»Ö»µē×ÓĀģŅĻQĒ”ŗĆ“ÓAµć³ö·¢£¬ŅŌ2øöµ„Ī»/ĆėµÄĖŁ¶ČĻņÓŅŌĖ¶Æ£¬ÉčĮ½Ö»µē×ÓĀģŅĻŌŚŹżÖįÉĻµÄCµćĻąÓö£¬ĒóCµć¶ŌÓ¦µÄŹżŹĒ¶ąÉŁ.
£Ø3£©Čōµ±µē×ÓĀģŅĻP“ÓBµć³ö·¢Ź±£¬ŅŌ3øöµ„Ī»/ĆėµÄĖŁ¶ČĻņ×óŌĖ¶Æ£¬Ķ¬Ź±ĮķŅ»Ö»µē×ÓĀģŅĻQĒ”ŗĆ“ÓAµć³ö·¢£¬ŅŌ2øöµ„Ī»/ĆėµÄĖŁ¶ČĻņÓŅŌĖ¶Æ£¬Ēó¾¹ż¶ą³¤µÄŹ±¼äĮ½Ö»µē×ÓĀģŅĻŌŚŹżÖįÉĻĻą¾ą35øöµ„Ī»³¤¶Č.
”¾“š°ø”æ(1)40;(2)30;£Ø3£©¾¹ż13Ćė»ņ27Ćė
”¾½āĪö”æ
£Ø1£©ĻČĒó³öA”¢BĮ½µćÖ®¼äµÄ¾ąĄė£ŗ90-£Ø-10£©=100£¬ŌŁĒó³öMµćµ½A”¢BĮ½µćµÄ¾ąĄė£ŗ100”Ā2=50£¬Č»ŗó½čÖśŹżÖį¼“æÉĒó³öMµć£®£Ø2£©øł¾ŻA”¢BĮ½µćµÄ¾ąĄėŗĶĮ½Ö»ĀģŅĻµÄŌĖ¶ÆĖŁ¶ČæÉĒó³öĻąÓöµÄŹ±¼ä£¬¼“æÉĒó³öĆæøöĀģŅĻŌĖ¶ÆµÄ¾ąĄė£¬¼“æÉĒó³öC¶ŌÓ¦µÄŹż.£Ø3£©“ĖĪŹ·ÖĪŖ2Ö»µē×ÓĀģŅĻĻąÓöĒ°Ļą¾ą35øöµ„Ī»³¤¶ČŗĶĻąÓöŗóĻą¾ą35øöµ„Ī»³¤¶Č£¬·Ö±š¼ĘĖć¼“æÉ.
£Ø1£©90-£Ø-10£©=100£¬
100”Ā2=50£¬
90-50=40.
“š£ŗMµć¶ŌÓ¦µÄŹżŹĒ40.
£Ø2£©100£Ø2+3£©=20£¬
20![]() 3=60£¬
3=60£¬
90-60=30.
“š£ŗCµć¶ŌÓ¦µÄŹżŹĒ30
£Ø3£©£Ø100-35£©”Ā£Ø2+3£©=13Ćė£¬
£Ø100+35£©”Ā£Ø2+3£©=27.
“š£ŗ¾¹ż13Ćė»ņ27ĆėĮ½Ö»µē×ÓĀģŅĻŌŚŹżÖįÉĻĻą¾ą35øöµ„Ī»³¤¶Č.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠ¼×”¢ŅŅĮ½øö²»ĶøĆ÷µÄ²¼“ü£¬¼×“ü֊װӊ3øöĶźČ«ĻąĶ¬µÄŠ”Ēņ£¬·Ö±š±źÓŠŹż×Ö0£¬1£¬2£»ŅŅ“ü֊װӊ3øöĶźČ«ĻąĶ¬µÄŠ”Ēņ£¬·Ö±š±źÓŠŹż×Ö©1£¬©2£¬0£®Ļ֓ӼדüÖŠĖ껜³éČ”Ņ»øöŠ”Ēņ£¬¼ĒĀ¼±źÓŠµÄŹż×ÖĪŖx£¬ŌŁ“ÓŅŅ“üÖŠĖ껜³éČ”Ņ»øöŠ”Ēņ£¬¼ĒĀ¼±źÓŠŹż×ÖĪŖy£¬Č·¶ØµćM×ų±źĪŖ£Øx£¬y£©£®
£Ø1£©ÓĆŹ÷דĶ¼»ņĮŠ±ķ·ØĮŠ¾ŁµćMĖłÓŠæÉÄܵÄ×ų±ź£®
£Ø2£©ĒóµćM£Øx£¬y£©ŌŚŗÆŹży=©x2©1µÄĶ¼ĻóÉĻµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćA£Øm£¬m£©ŌŚµŚŅ»ĻóĻŽ£¬ĒŅŹµŹżmĀś×ćĢõ¼ž£ŗ![]() £¬AByÖįÓŚB£¬ACxÖįÓŚC
£¬AByÖįÓŚB£¬ACxÖįÓŚC
£Ø1£©ĒómµÄÖµ£»
£Ø2£©ČēĶ¼1£¬BE=1£¬¹żA×÷AF”ĶAE½»xÖįÓŚF£¬Į¬EF£¬DŌŚAOÉĻ£¬ĒŅAD=AE£¬Į¬½ÓED²¢ŃÓ³¤½»xÖįÓŚµćP£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©ČēĶ¼2£¬GĪŖĻ߶ĪOCŃÓ³¤ĻßÉĻŅ»µć£¬AC=CG£¬EĪŖĻ߶ĪOBÉĻŅ»¶Æµć£Ø²»ÓėO”¢BÖŲŗĻ£©£¬FĪŖĻ߶ĪCEµÄÖŠµć£¬ČōBF”ĶFK½»AGÓŚK£¬ŃÓ³¤BF”¢AC½»ÓŚM£¬Į¬½ÓKM£®ĒėĪŹ”ĻFBKµÄ“󊔏Ē·ń±ä»Æ£æČō²»±ä£¬ĒėĒóĘäÖµ£»Čōøı䣬Ēó³ö±ä»ÆµÄ·¶Ī§£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij»ī¶ÆÖŠŠÄ×¼±ø“ų»įŌ±Č„ĮśĢ¶“óĻæ¹ČŅ»ČÕÓĪ£¬1ÕŶłĶÆʱŗĶ2ÕųÉČĖʱ¹²Šč190ŌŖ£¬2ÕŶłĶÆʱŗĶ3ÕųÉČĖʱ¹²Šč300ŌŖ£®½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĒóĆæÕŶłĶÆʱŗĶĆæÕųÉČĖʱø÷¶ąÉŁŌŖ£æ
£Ø2£©Õāøö»ī¶ÆÖŠŠÄĻė“ų50ČĖČ„ÓĪĶę£¬·ŃÓĆ²»³¬¹ż3000ŌŖ£¬²¢ĒŅ³öÓŚ°²Č«æ¼ĀĒ£¬¶łĶÆČĖŹż²»Äܳ¬¹ż22ČĖ£¬ĒėÄć°ļÖś»ī¶ÆÖŠŠÄČ·Į¢³öÓĪ·½°ø£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
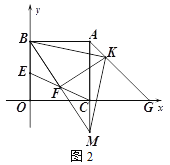
”¾ĢāÄæ”æČēĶ¼¢Ł£¬¾ŲŠĪÖ½Ę¬ABCDµÄ±ß³¤·Ö±šĪŖa”¢b£Øa£¼b£©£¬µćM”¢N·Ö±šĪŖ±ßAD”¢BCÉĻĮ½µć£ØµćA”¢C³żĶā£©£¬Į¬½ÓMN£®
£Ø1£©ČēĶ¼¢Ś£¬·Ö±šŃŲME”¢NF ½«MNĮ½²ąÖ½Ę¬ÕŪµž£¬Ź¹µćA”¢C·Ö±šĀäŌŚMNÉĻµÄA”䔢C”䓦£¬Ö±½ÓŠ“³öMEÓėFNµÄĪ»ÖĆ¹ŲĻµ£»
£Ø2£©ČēĶ¼¢Ū£¬µ±MN”ĶBC Ź±£¬ČŌ°“£Ø1£©ÖŠµÄ·½Ź½ÕŪµž£¬ĒėĒó³öĖıߊĪA”äEBNÓėĖıߊĪC”äFDM µÄÖܳ¤£ØÓĆŗ¬aµÄ“śŹżŹ½±ķŹ¾£©£¬²¢ÅŠ¶ĻĖıߊĪA”äEBNÓėĖıߊĪC”äFDMÖܳ¤Ö®¼äµÄŹżĮæ¹ŲĻµ£»
£Ø3£©ČēĶ¼¢Ü£¬Čō¶Ō½ĒĻßBDÓėMN½»ÓŚµćO£¬·Ö±šŃŲBM”¢DN½«MNĮ½²ąÖ½Ę¬ÕŪµž£¬ÕŪµžŗ󣬵ćA”¢CĒ”ŗƶ¼ĀäŌŚµćO“¦£¬²¢ĒŅµĆµ½µÄĖıߊĪBNDMŹĒĮāŠĪ£¬ĒėÄćĢ½Ė÷a”¢bÖ®¼äµÄŹżĮæ¹ŲĻµ.
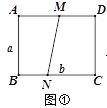
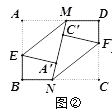
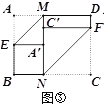

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻČ»Æ¼ņ£¬ŌŁĒóÖµ£ŗ
£Ø1£©£Øx+2£©£Øx©3£©©x£Øx©4£©£¬ĘäÖŠx=© ![]()
£Ø2£©£Øa+b£©£Øa©b£©+£Øa+b£©2©2a2 £¬ ĘäÖŠa=3£¬b=© ![]() £®
£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŹżŃ§Š”×éµÄ10Ī»Ķ¬Ń§Õ¾³ÉŅ»ĮŠ×ö±ØŹżÓĪĻ·£¬¹ęŌņŹĒ£ŗ“ÓĒ°Ć굌Ņ»Ī»Ķ¬Ń§æŖŹ¼£¬ĆæĪ»Ķ¬Ń§ŅĄ“Ī±Ø×Ō¼ŗĖ³ŠņŹżµÄµ¹ŹżµÄ2±¶¼Ó1£¬µŚ1Ī»Ķ¬Ń§±Ø£Ø ![]() +1£©£¬µŚ2Ī»Ķ¬Ń§±Ø£Ø
+1£©£¬µŚ2Ī»Ķ¬Ń§±Ø£Ø ![]() +1£©£¬µŚ3Ī»Ķ¬Ń§±Ø£Ø
+1£©£¬µŚ3Ī»Ķ¬Ń§±Ø£Ø ![]() +1£©”ÕāŃłµĆµ½µÄnøöŹżµÄ»żĪŖ £®
+1£©”ÕāŃłµĆµ½µÄnøöŹżµÄ»żĪŖ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓÉÓŚ»»¼¾£¬Ņ»¼Ņ·ž×°µźµÄĄĻ°åĻė½«Ä³·ž×°“ņÕŪĻśŹŪ£¬ÓŚŹĒĖżŗĶÕżŌŚÉĻĘßÄź¼¶µÄ¶ł×ÓÉĢĮæ“ņÕŪ·½°ø£¬ĻĀĆęŹĒĖżŗĶ¶ł×ÓÉĢĮæŹ±µÄ¶Ō»°Ēé¾°£ŗ
ĀčĀč£ŗ”°¶ł×Ó£¬Ć漞ŅĀ·ž°“±ź¼ŪµÄ5ÕŪ³öŹŪ£¬æÉŅŌĀš£æ”±
¶ł×Ó£ŗ”°ČōĆ漞ŅĀ·ž°“±ź¼ŪµÄ5ÕŪ³öŹŪ»įæ÷±¾30ŌŖ.”±
ĀčĀč£ŗ”°ÄĒĆ漞ŅĀ·ž°“±ź¼ŪµÄ8ÕŪ³öŹŪÄŲ£æ”±
¶ł×Ó£ŗ”°ČōĆ漞ŅĀ·ž°“±ź¼ŪµÄ8ÕŪ³öŹŪ½«»į׬60ŌŖ.”±
””
Ēėøł¾ŻÉĻĆęµÄŠÅĻ¢£¬½ā¾öĪŹĢā£ŗ
£Ø1£©ĒóÕāÖÖ·ž×°µÄ±ź¼Ū.
£Ø2£©ČōŅŖ²»æ÷±¾£¬ÖĮÉŁ“ņ¼øÕŪ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µČŃüÖ±½ĒČż½ĒŠĪ![]() µÄÖ±½Ē¶„µć
µÄÖ±½Ē¶„µć![]() ŌŚµŚŅ»ĻóĻŽ£¬¶„µć
ŌŚµŚŅ»ĻóĻŽ£¬¶„µć![]() ”¢
”¢![]() ·Ö±šŌŚŗÆŹż
·Ö±šŌŚŗÆŹż![]() Ķ¼ĻńµÄĮ½øö·ÖÖ§ÉĻ£¬ĒŅ
Ķ¼ĻńµÄĮ½øö·ÖÖ§ÉĻ£¬ĒŅ![]() ¾¹żŌµć
¾¹żŌµć![]() £¬
£¬![]() Óė
Óė![]() ÖįĻą½»ÓŚµć
ÖįĻą½»ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬ŅŃÖŖ
£¬ŅŃÖŖ![]() Ę½·ÖĖıߊĪ
Ę½·ÖĖıߊĪ![]() µÄĆ껿.
µÄĆ껿.
(1)Ö¤Ć÷:![]() :
:
(2)Ēóµć![]() µÄ×ų±ź.
µÄ×ų±ź.

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com