
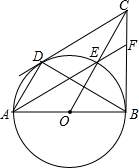
 如图,在Rt△BOC 中,以OB为半径的⊙O交斜边OC于点E,AB是⊙O的直径,过点A作AD∥OC交⊙O于点D,连接BD、CD、AE,延长AE交BC于点F.下列结论:①CD是⊙O的切线;②OC垂直平分BD;③点E是△BCD的内心;④EF=CF,其中一定成立的是( )
如图,在Rt△BOC 中,以OB为半径的⊙O交斜边OC于点E,AB是⊙O的直径,过点A作AD∥OC交⊙O于点D,连接BD、CD、AE,延长AE交BC于点F.下列结论:①CD是⊙O的切线;②OC垂直平分BD;③点E是△BCD的内心;④EF=CF,其中一定成立的是( )| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
分析 连接OD,由等腰三角形的性质和平行线的性质得出∠COD=∠COB,由SAS证明△COD≌△COB,得出∠CDO=∠CBO=90°,得出①成立;由等腰三角形的三线合一性质得出②成立;由垂径定理得出$\widehat{DE}=\widehat{BE}$,由弦切角定理和圆周角定理得出∠CBE=∠BAE,∠BAE=∠DBE,得出∠CBE=∠DBE,得出点E是△BCD的内心,③成立;④不成立;即可得出结果.
解答 解:连接OD,如图所示:
∵OB、OD为⊙O的半径,
∴OB=OD,
∴∠OAD=∠ODA.
∵AD∥OC,
∴∠OAD=∠COB,∠ODA=∠COD,
∴∠COD=∠COB.
在△CDO和△CBO中,$\left\{\begin{array}{l}{OD=OB}&{\;}\\{∠COD=∠COB}&{\;}\\{OC=OC}&{\;}\end{array}\right.$,
∴△COD≌△COB(SAS),
∴∠CDO=∠CBO=90°,CD=CB,∠DCO=∠BCO,
∴OD⊥CD,
∴CD是⊙O的切线,
∴①成立;
∵CD=CB,∠DCO=∠BCO,
∴OC垂直平分BD,
∴②成立,
连接BE,
∵OC垂直平分BD,
∴$\widehat{DE}=\widehat{BE}$,
∴∠CBE=∠BAE,∠BAE=∠DBE,
∴∠CBE=∠DBE,
∴BE平分∠DBC,
又∵∠DCO=∠BCO,
∴CE平分∠BCD,
∴点E是△BCD的内心,
∴③成立;
∵没有条件得出∠CEF=∠ECF,
∴EF与CF不一定相等,
∴④不成立;
成立的是①②③.
故选:A.
点评 本题考查了切线的判定、全等三角形的判定与性质、平行线的性质、等腰三角形的性质、弦切角定理、圆周角定理等知识;本题综合性强,有一定难度,需要证明三角形全等和运用弦切角定理、圆周角定理等知识才能得出结果.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “明天降雨的概率是80%”表示明天有80%的时间降雨 | |
| B. | “抛一枚硬币正面向上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上 | |
| C. | “彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖 | |
| D. | 班级里40名同学中,至少有三人出生在同一月份 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{2x-y=-3}\\{4x+y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x-y=-6}\\{2x+y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=-2}\\{x+2y=2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中正确的是②③(填编号)
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中正确的是②③(填编号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com