

分析 (1)由C类有6人,占30%,即可求得总人数,继而求得A与D类人数,补全统计图;
(2)由中位数与平均数的定义,可求得该小组每人制作陶艺作品数量的中位数与平均数;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲乙丙三人制作的第一件作品是同一个对象的情况,再利用概率公式即可求得答案.
解答 解:(1)∵C类有6人,占30%,
∴这个活动小组共有:6÷30%=20(人),
B占:8÷20=40%,
∴A类占:1-10%-30%-40%=20%,
∴A类:20×20%=4(人),D类:20×10%=2(人);
故答案为:20;
补全统计图: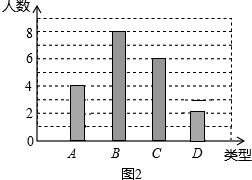
(2)中位数5件;
平均数为:$\frac{4×4+8×5+6×6+2×7}{20}$=5.3件;
故答案为:5,5.3;
(3)画树状图得: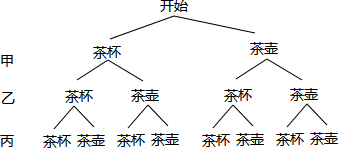
∵共有8种等可能的结果,其中甲乙丙三人制作的第一件作品是同一个对象的有2种情况,
∴甲乙丙三人制作的第一件作品是同一个对象的概率是:$\frac{2}{8}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 此题考查了列表法或树状图法求概率以及扇形与条形统计图的知识.注意概率=所求情况数与总情况数之比.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
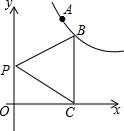 已知点A(1,2)、点B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点
已知点A(1,2)、点B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
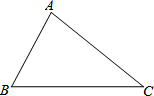 (1)如图,试用直尺与圆规在平面内确定一点O,使得点O到△ABC的两边AB、AC的距离相等,并且点O到B、C两点的距离也相等.(不写作法,但需保留作图痕迹)
(1)如图,试用直尺与圆规在平面内确定一点O,使得点O到△ABC的两边AB、AC的距离相等,并且点O到B、C两点的距离也相等.(不写作法,但需保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
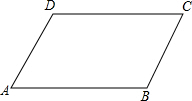 如图,已知平行四边形ABCD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示下列向量:
如图,已知平行四边形ABCD,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$表示下列向量:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com